3.3 Zastosowania
3.3.1 Gra w chaos i genetyka
Czytelniku, poświęć chwilę, by zastanowić się nad konsekwencjami ostatniego przykładu. Dobierając różne prawdopodobieństwa, otrzymujemy wizualnie inne figury. W nieskończoności cały fraktal by się wysycił, ale przy skończonej liczbie kroków gęstość punktów koduje informacje o rozkładzie losowanych transformacji.
Ta obserwacja przyczyniła się do szeregu ciekawych zastosowań gry w chaos do kodowania informacji w sekwencjach o różnej długości. Okazuje się, że na fraktale możemy ,,nawijać’’ ciągi pozornie losowych symboli tak by wizualnie badać częstości względnego występowania tych symboli.
Przyjrzyjmy się zastosowaniu tego pomysłu do kodowania sekwencji genetycznych. Sekwencje składają się z ciągów liter A, C, T i G. Rozważmy cztery transformacje polegające na dwukrotnym zmniejszeniu i przesunięciu w stronę jednego z rogów kwadratu.
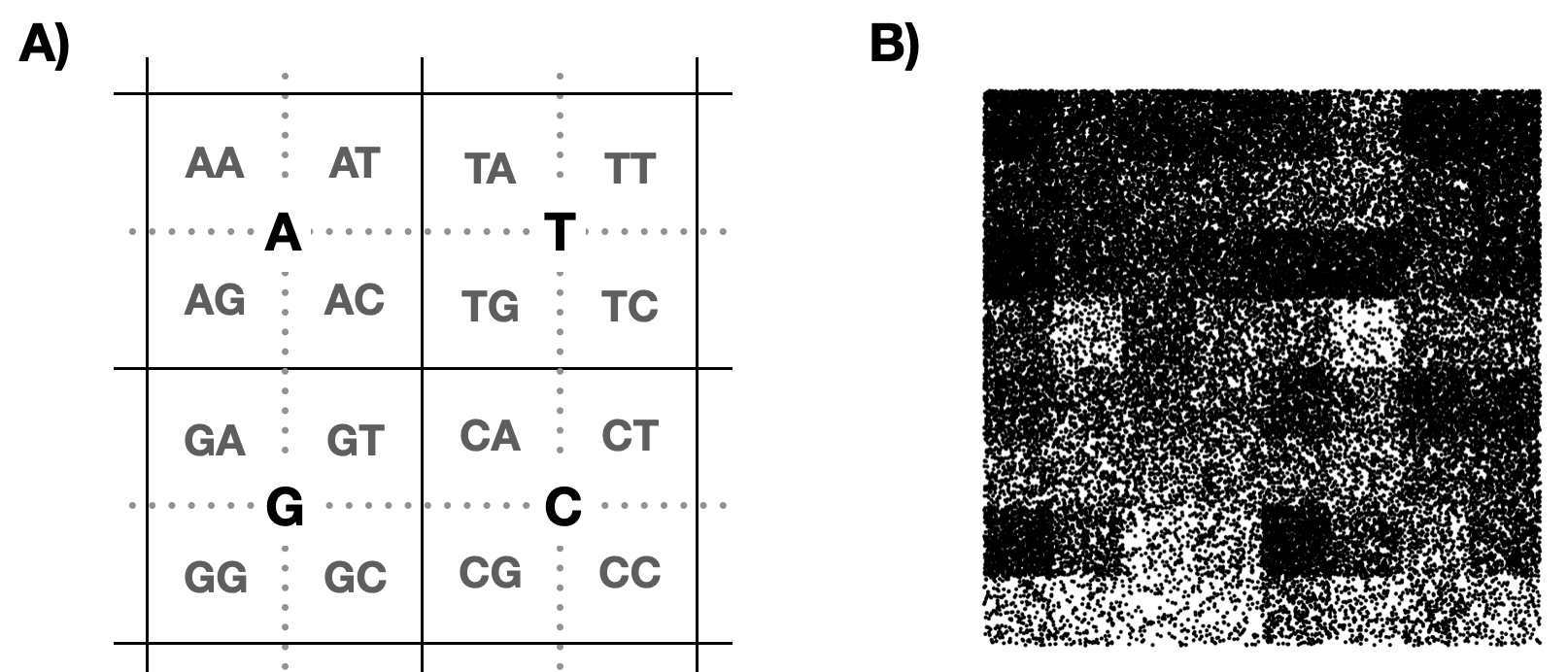
Gra w chaos na sekwencjach biologicznych. Lewy panel ilustruje metodę działania kodowania. Prawy panel koduje sekwencję genetyczną wirusa SARS-CoV-2
Teraz zamiast losować transformację, możemy czytać jakąś sekwencję genetyczną i wybierać transformację w zależności od napotkanej litery lub ciągu liter. Dzięki temu często występujące wzorce w sekwencji będą wizualnie zakodowane we fraktalu.
Powyższy przykład koduje sekwencję wirusa SARS-CoV-2 za pomocą czterech transformacji. Inne pomysły na kodowanie sekwencji biologicznych z użyciem gry w chaos można znaleźć w artykule Chaos game representation and its applications in bioinformatics [LöHe21].
3.3.2 Gra w chaos i muzyka
Zastosowań dla matematyki fraktalnej szukano również w muzyce. W literaturze, zarówno naukowej, jak i popularnonaukowej, można znaleźć liczne przykłady różnorodnych prób połączenia muzyki z fraktalami. Począwszy od wykorzystywania fraktali do generowania muzyki, która nie jest ani zbyt monotonna, ani zbyt chaotyczna, po zastosowanie fraktali do badania przewidywalności różnych gatunków muzycznych [K.Hs91].
Przykładowo, w roku 2012 w popularnym magazynie ,,Wired’’ zaprezentowano analizę fraktalną różnych utworów muzycznych. Utwory zostały najpierw opisane w języku składowych harmonicznych, a następnie przeprowadzono na nich analizę wymiaru fraktalnego, stwierdzając, że najbardziej przewidywalne są symfonie, a najmniej przewidywalne są utwory ragtime.
3.3.3 Wymiar fraktalny mózgu
W poprzednim rozdziale przedstawiliśmy definicję wymiaru pudełkowego. Myliłby się ten, kto założy, że będzie ona wykorzystywana jedynie do fraktali. Praktycy znaleźli dla niej wiele ciekawych zastosowań, jak np. mierzenie stopnia poszarpania linii brzegowej różnych państw. Przykładowo wymiar pudełkowy wybrzeża Australii wynosi 1,143 (według Fractal dimension of coastline of Australia. [HRBS21]), co świadczy o dużej nieregularności. To jednak znacznie mniej niż wymiar bardzo poszarpanego wybrzeża Norwegii, który wynosi 1,3727.
Udało się również zmierzyć wymiary fraktalne obiektów anatomicznych, takich jak mózg czy płuca. Okazuje się, że powierzchnia mózgu ma wymiar 2,79, będący dowodem dużego pofałdowania tego organu. Powierzchnia płuc ma jeszcze wyższy wymiar, dochodzący do wartości 2,97 (według List of fractals by Hausdorff dimension [Wiki22]). W literaturze medycznej znaleźć można przykłady analiz wykorzystujących wymiar fraktalny określonych struktur anatomicznych w detekcji chorób.
Poniżej przedstawiamy rysunek z artykułu Fractal Analysis of Lung Structure in Chronic Obstructive Pulmonary Disease [TSSH20] poświęconego użyciu wymiaru fraktalnego w analizie przewlekłej choroby płuc. Przewlekłe choroby mogą prowadzić do zmian struktur anatomicznych, które można ilościowo opisać wymiarem fraktalnym. Pomaga to zarówno zrozumieć zmiany wywołane chorobą, jak i budować modele predykcyjne wspierające diagnostykę.
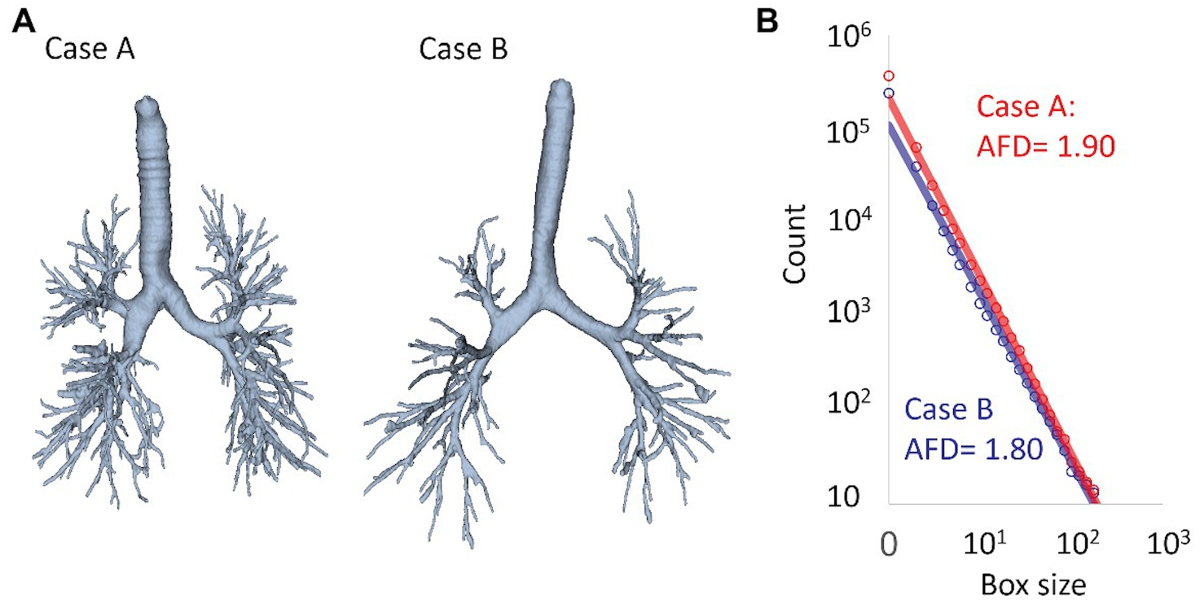
Wykres z pracy Fractal analysis of lung structure in chronic obstructive pulmonary disease, badającej możliwość użycia wymiaru fraktalnego naczyń krwionośnych płuc w analizie chorób przewlekłych płuc. Panel A pokazuje schematyczne struktury głównych naczyń krwionośnych, panel B przedstawia, jak liczba pudełek rośnie z malejącą wielkością boku pudełka
Gdzie jeszcze można zastosować geometrię fraktalną? Z pewnością jeszcze wiele ciekawych odkryć przed nami.