4.4 Drzewa

Składając kilka transformacji, możemy uzyskać bardziej złożone i bardziej kontrolowane fraktale.
Poniżej zamieszczamy przykłady dwóch fraktali wyglądających jak drzewa. Pierwszy złożony jest z pięciu, a drugi z siedmiu transformacji. Gdy już dostrzeże się ideę stojącą za konstrukcją drzewa, łatwo zaproponować własne zmiany i rozszerzenia.
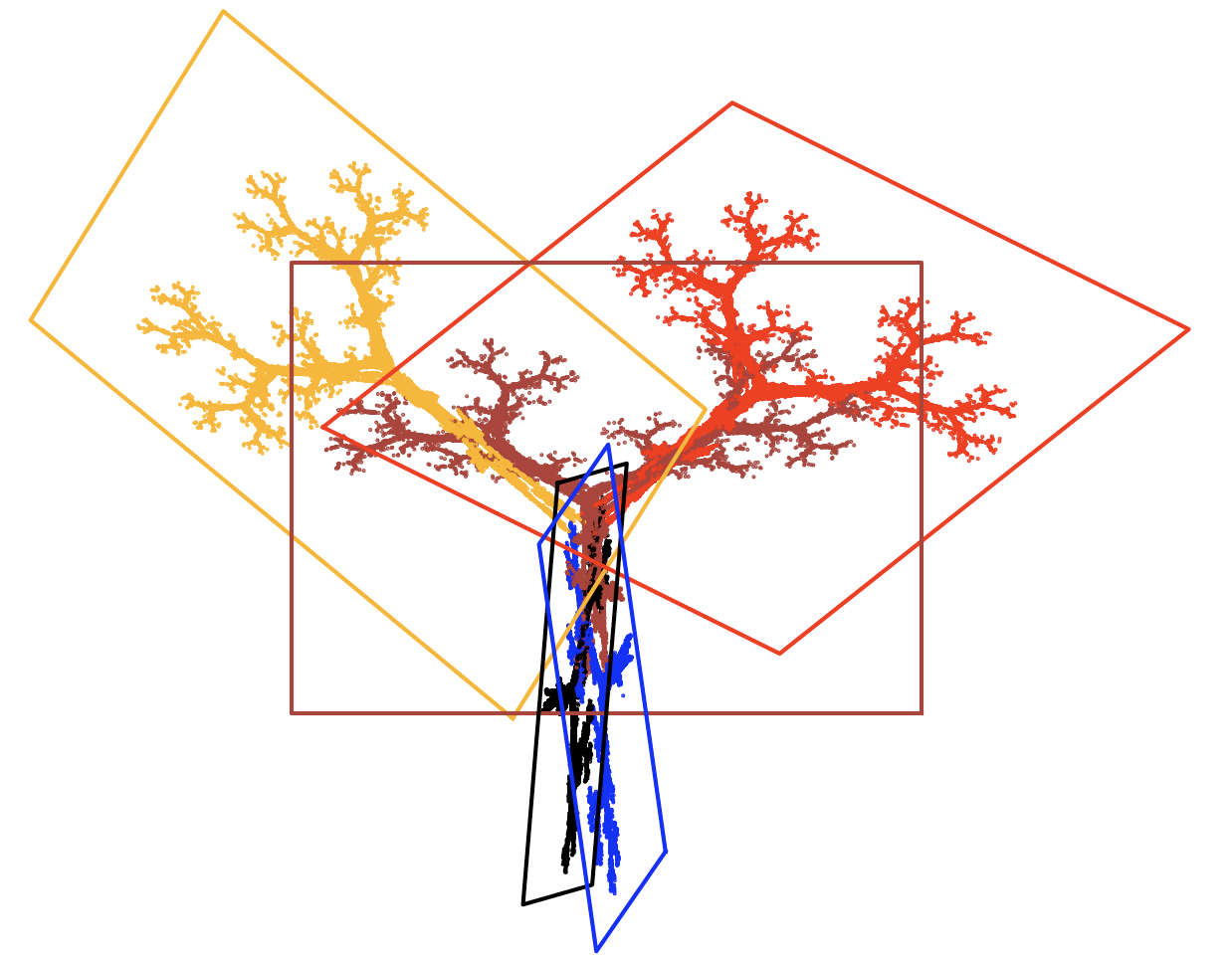
Składowe transformacje dla liścia klonu. Kolorem oznaczono obrazy kolejnych transformacji.
Każda transformacja losowana jest z równym prawdopodobieństwem \(1/5\).
\[ f_1(x, y) = \begin{bmatrix} 0,195 & -0,488 & 0,4431 \\ 0,344 & 0,443 & 0,2452 \end{bmatrix} [x \ y \ 1]^T \] \[ f_2(x, y) = \begin{bmatrix} 0,462 & 0,414 & 0,2511 \\ -0,252 & 0,361 & 0,5692 \end{bmatrix} [x \ y \ 1]^T \] \[ f_3(x, y) = \begin{bmatrix} -0,637 & 0 & 0,8562 \\ 0 & 0,501 & 0,2512 \end{bmatrix} [x \ y \ 1]^T \] \[ f_4(x, y) = \begin{bmatrix} -0,035 & 0,07 & 0,4884 \\ -0,469 & 0,022 & 0,507 \end{bmatrix} [x \ y \ 1]^T \] \[ f_5(x, y) = \begin{bmatrix} -0,058 & -0,07 & 0,597 \\ 0,453 & -0,111 & 0,097 \end{bmatrix} [x \ y \ 1]^T \]

Niektóre transformacje nakładają się na siebie, by uzyskać efekt grubszego pnia lub grubszej gałęzi.
Fragmenty tego drzewa można dodatkowo rozjaśnić lub przyciemnić, zmieniając prawdopodobieństwo wylosowania transformacji.
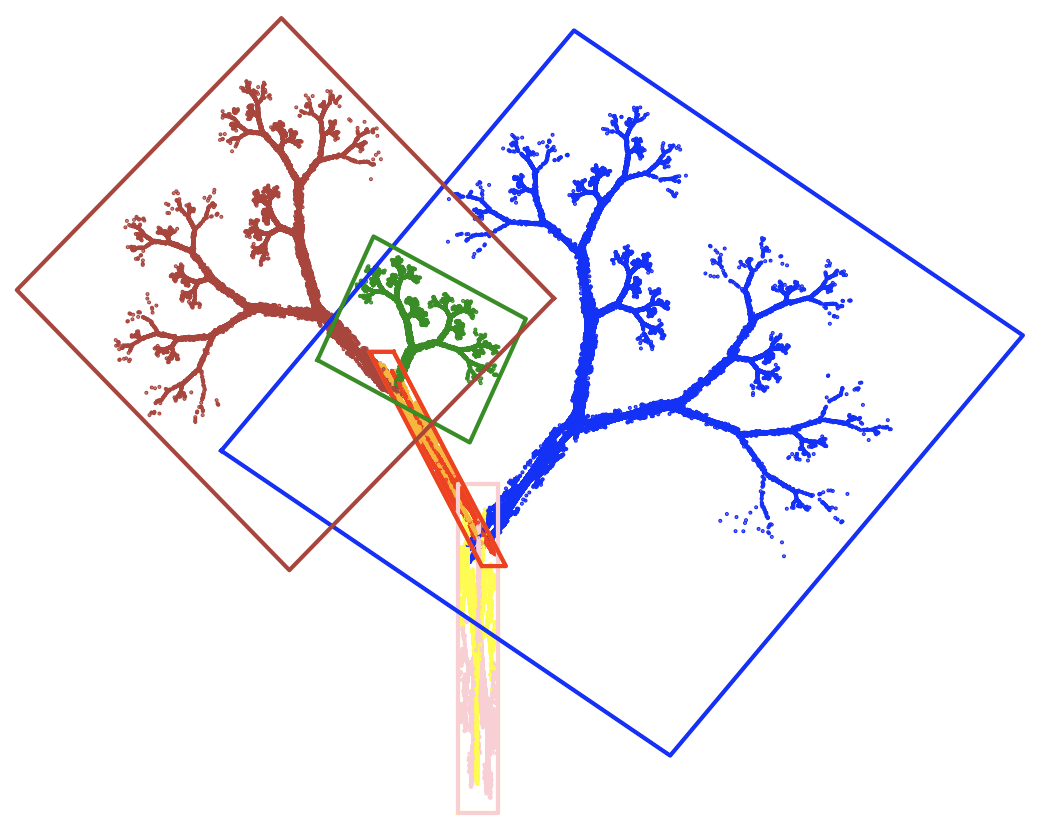
Składowe transformacje dla liścia klonu. Kolorem oznaczono obrazy kolejnych transformacji.
Każda transformacja losowana jest z równym prawdopodobieństwem \(1/7\).
\[ f_1(x, y) = \begin{bmatrix} 0,05 & 0 & -0,06\\ 0 & 0,4 & -0,47 \end{bmatrix} [x \ y \ 1]^T \] \[ f_2(x, y) = \begin{bmatrix} -0,05 & 0 & -0,06 \\ 0 & -0,4 & -0,47 \end{bmatrix} [x \ y \ 1]^T \] \[ f_3(x, y) = \begin{bmatrix} 0,03 & -0,14 & -0,16 \\ 0 & 0,26 & -0,01 \end{bmatrix} [x \ y \ 1]^T \] \[ f_4(x, y) = \begin{bmatrix} -0,03 & 0,14 & -0,16 \\ 0 & -0,26 & -0,01 \end{bmatrix} [x \ y \ 1]^T \] \[ f_5(x, y) = \begin{bmatrix} 0,56 & 0,44 & 0,3 \\ -0,37 & 0,51 & 0,15 \end{bmatrix} [x \ y \ 1]^T \] \[ f_6(x, y) = \begin{bmatrix} 0,19 & 0,07 & -0,2 \\ -0,1 & 0,15 & 0,28 \end{bmatrix} [x \ y \ 1]^T \] \[ f_7(x, y) = \begin{bmatrix} -0,33 & -0,34 & -0,54 \\ -0,33 & 0,34 & 0,39 \end{bmatrix} [x \ y \ 1]^T \]