4.7 Smoki


W drugim rozdziale poznaliśmy smoka Heighwaya i drzewo pitagorejskie. Okazuje się, że oba te fraktale należą do bogatszej rodziny, którą można sparametryzować jedną liczbą. Dla każdego \(T \in [0,1]\) można określić taką parę.
\[ f_1(x, y) = \frac{1}{\sqrt{2}} \begin{bmatrix} \cos(\pi/4) & -\sin(\pi/4) \\ \sin(\pi/4) & \cos(\pi/4) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \] \[ f_2(x, y) = \frac{1}{\sqrt{2}} \begin{bmatrix} \cos\left(\frac 34 \pi - \frac{T}2 \pi\right) & -\sin\left(\frac 34 \pi - \frac{T}2 \pi\right) \\ \sin\left(\frac 34 \pi - \frac{T}2 \pi\right) & \cos\left(\frac 34 \pi - \frac{T}2 \pi\right) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} 1 - T/2 \\ T/2 \end{bmatrix} \]
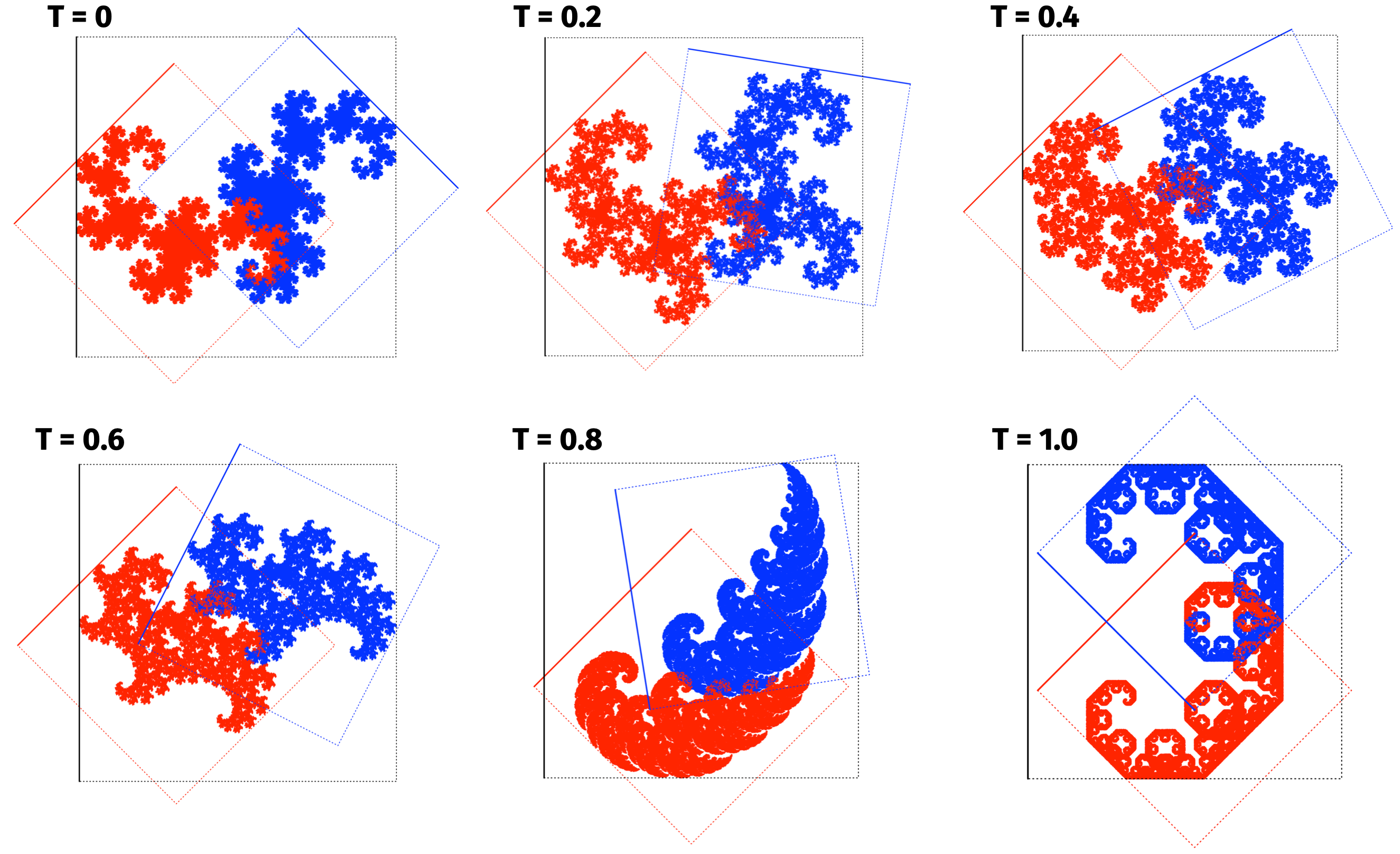
Poniżej pokazano sześć fraktali z tej rodziny.