1.6 Przykłady w języku Julia

Tworząc fraktale pewne operacje musimy powtarzać w nieskończoność, lub przynajmniej bardzo długo. Świetnie się do tego nadają wydajne, elastyczne i bardzo bardzo szybkie języki programowania. Takim właśnie językiem jest Julia. Interpreter tego języka i dokumentację można pobrać ze strony [https://julialang.org/]. Poniżej prezentujemy kilka informacji, które pomogą w zrozumieniu kolejnych przykładów.

1. Poniższe przykłady korzystają z biblioteki Plots, podstawowej biblioteki dla języka Julia. Funkcja plot() z tej biblioteki tworzy pusty wykres. Można do niego dorysować kolejne figury funkcją plot!(). W poniższych przykładach tak będziemy tworzyć dodatkowe wypełnione wielokąty, trójkąty i kwadraty.
2. Julia to język bardzo przyjazny operacjom matematycznym, można bez dodatkowych modułów korzystać z funkcji matematycznych, takich jak sqrt(). Operatory arytmetyczne takie jak + czy / działają zarówno dla liczb jak i dla wektorów.
3. Aby kod był bardziej czytelny korzystamy z rekurencji, a więc konstrukcji, w której funkcja, sama się wywołuje. Nowe funkcje definiuje się z użyciem słowa function. W przypadku krótszych funkcji można stosować uproszczoną definicje z operatorem =. Z krótszego sposobu skorzystamy definiując funkcje line, triangle, square.

1.6.1 Kurz Cantora

Rysowanie fraktali rozpocznijmy od Kurzu Cantora. Wykorzystamy do tego rekurencyjną funkcję dust, która przyjmuje trzy argumenty: x – początek fraktala, scale – wielkość fraktala oraz depth – aktualny poziom zagnieżdżenia fraktala.

# Pakiet z funkcjami graficznymi.
using Plots 

# Funkcja definiująca odcinek.
line(x, scale) = Shape([x, x+scale], [0, 0]) 

# Rekurencyjna funkcja do rysowania kurzu. 
# Jeżeli depth=1, to rysujemy odcinek, jeżeli depth>1, 
# to rysujemy dwa kurze Cantora obok siebie.
function dust(x, scale, depth=1) 
    if depth == 0 
        plot!(line(x, scale), color=:black, legend=:false)
    else 
      dust(x, scale/3, depth - 1)
      dust(x + scale*2/3, scale/3, depth-1)
    end
end

# Czyścimy ekran i zaczynamy rysowanie kurzu.
plot(0, xlim=(-0.1,1.1), ylim=(-0.1,0.1), axis=nothing) 
dust(0.0, 1.0, 4)

Wynik wykonania powyższych instrukcji

1.6.2 Trójkąt Sierpińskiego

Czas na kultowy trójkąt Sierpińskiego. Aby go narysować wykorzystamy rekurencyjną funkcję sierpinski(), która przyjmuje trzy argumenty: x, y – miejsce od którego należy rysować fraktal, scale – wielkość fraktalu oraz depth aktualny poziom zagnieżdżenia fraktala.

triangle(x, y, scale) = Shape([x, x+scale, x+scale/2, x],
      [y, y, y+scale*sqrt(3)/2, y])

# Rekurencyjna funkcja do rysowania trójkąta Sierpińskiego. 
# Jeżeli depth=1, to rysujemy trójkąt używając funkcji triangle(),
# jeżeli depth>1. to rysujemy trzy trójkąty Sierpińskiego.
function sierpinski(x, y, scale, depth=1)
  if depth==0
    plot!(triangle(x,y,scale),color=:black,legend=:false)
  else
    sierpinski(x, y, scale/2, depth-1)
    sierpinski(x+scale/2, y, scale/2, depth-1)
    sierpinski(x+scale/4,y+sqrt(3)*scale/4,scale/2,depth-1)
  end
end

plot(0, xlim=(0,1), ylim=(0,1), axis=nothing)
sierpinski(0, 0, 1, 6)

Wynik wykonania powyższych instrukcji

1.6.3 Dywan Sierpińskiego

Konstrukcja fraktala zaproponowana przez Wacława Sierpińskiego może być powtórzona dla innych kształtów.

square(x, y, w) = Shape([x, x+w, x+w, x], [y, y, y+w, y+w])   

# Wykorzystujemy funkcje square zdefiniowaną powyżej aby narysować kwadrat.
function carpet(x, y, scale, depth=1)
  if depth==0
    plot!(square(x,y,scale), color=:black, legend=:false) 
  else
    carpet(x, y, scale/3, depth-1)
    carpet(x, y+scale, scale/3, depth-1)
    carpet(x, y+2scale, scale/3, depth-1)  
    carpet(x+scale, y, scale/3, depth-1)
    carpet(x+scale, y+2scale, scale/3, depth-1)
    carpet(x+2scale, y, scale/3, depth-1)
    carpet(x+2scale, y+scale, scale/3, depth-1)
    carpet(x+2scale, y+2scale, scale/3, depth-1)
  end
end

plot(0, xlim=(0,3), ylim=(0,3), axis=nothing)
carpet(0.0, 0.0, 1.0, 5)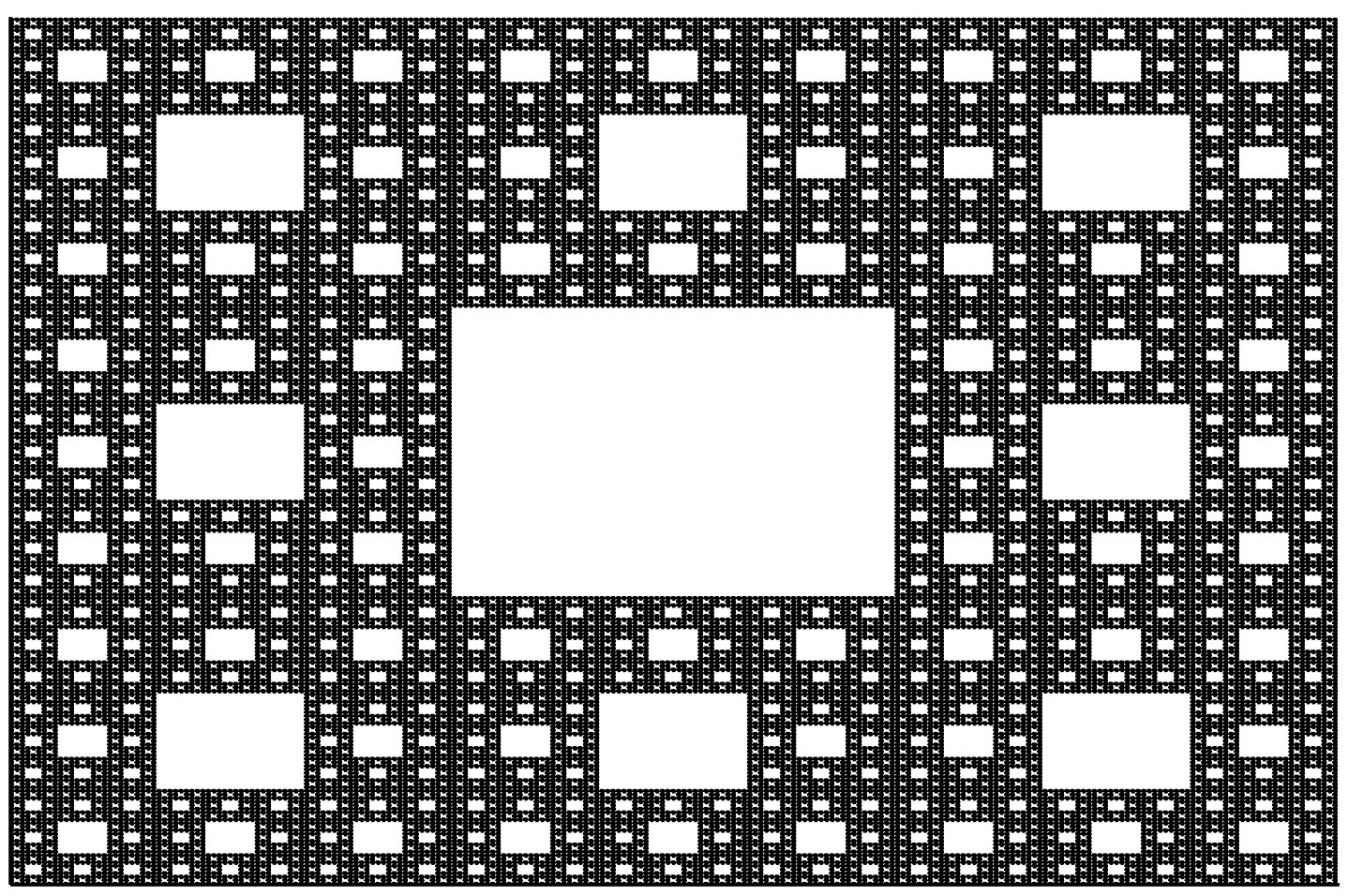

Wynik wykonania powyższych instrukcji