1.4 Przykłady w języku Python

W tym rozdziale przedstawiamy przykłady kodu w programie Python, które pozwalają na narysowanie kolejnych przybliżeń Kurzu Cantora, Trójkąta Sierpińskiego i Dywanu Sierpińskiego.

Każdy może opisywane fraktale odtworzyć na własnym komputerze. W tym celu można zainstalować interpreter języka Python. Kody generujące fraktale są krótkie i ich zrozumienie jest możliwe bez wcześniejszej znajomości tego języka, choć oczywiście warto ten język poznać. Kilka informacji, które pomogą w zrozumieniu kodów:

1. Poniższe przykłady korzystają z biblioteki matplotlib, w której znajdują się funkcje do rysowania, jak np. funkcja plot() do rysowania odcinka oraz fill() do rysowania wypełnionych wielokątów, tutaj trójkąta i kwadratu. Funkcja figure() tworzy pusty wykres, a show() wyświetla go na ekranie.
2. Bardziej złożone funkcje matematyczne znajdują się w bibliotece math. W tych przykładach wykorzystamy ją, aby użyć funkcji pierwiastka kwadratowego sqrt().
3. W bibliotece numpy znajdują się funkcje do operacji na wektorach i macierzach. Wykorzystamy ją, by uprościć zapis operacji na dwuelementowych wektorach – współrzędnych punktów.
4. W wielu miejscach korzystamy z rekurencji, a więc sytuacji, gdy funkcja wywołuje samą siebie. Nowe funkcje definiuje się z użyciem słowa kluczowego def. Jednym z argumentów przedstawionych funkcji rekurencyjnych jest depth – określa, ile razy funkcja ma się rekurencyjnie wywołać.

1.4.1 Kurz Cantora

Rysowanie kurzu Cantora oprzemy na rekurencyjnej funkcji dust, która przyjmuje trzy argumenty: x – miejsce, od którego należy rysować fraktal, scale – wielkość fraktala oraz depth – aktualny poziom zagnieżdżenia fraktala.

# Niezbędne biblioteki.
import matplotlib.pyplot as plt
import numpy as np

# Jeżeli depth=1 to rysujemy odcinek, jeżeli depth>1, 
# to rysujemy dwa małe kurze Cantora obok siebie.
def dust(x, scale, depth): 
    if depth > 1:  
        dust(x, scale / 3, depth - 1)
        dust(x + scale*2/3, scale / 3, depth - 1)
    else:
        plt.plot([x, x+scale], [0,0], color = "black")

# Inicjacja rysunku i narysowanie kurzu o głębokości 5.
plt.figure()
dust(0, scale = 1, depth = 5)
plt.show()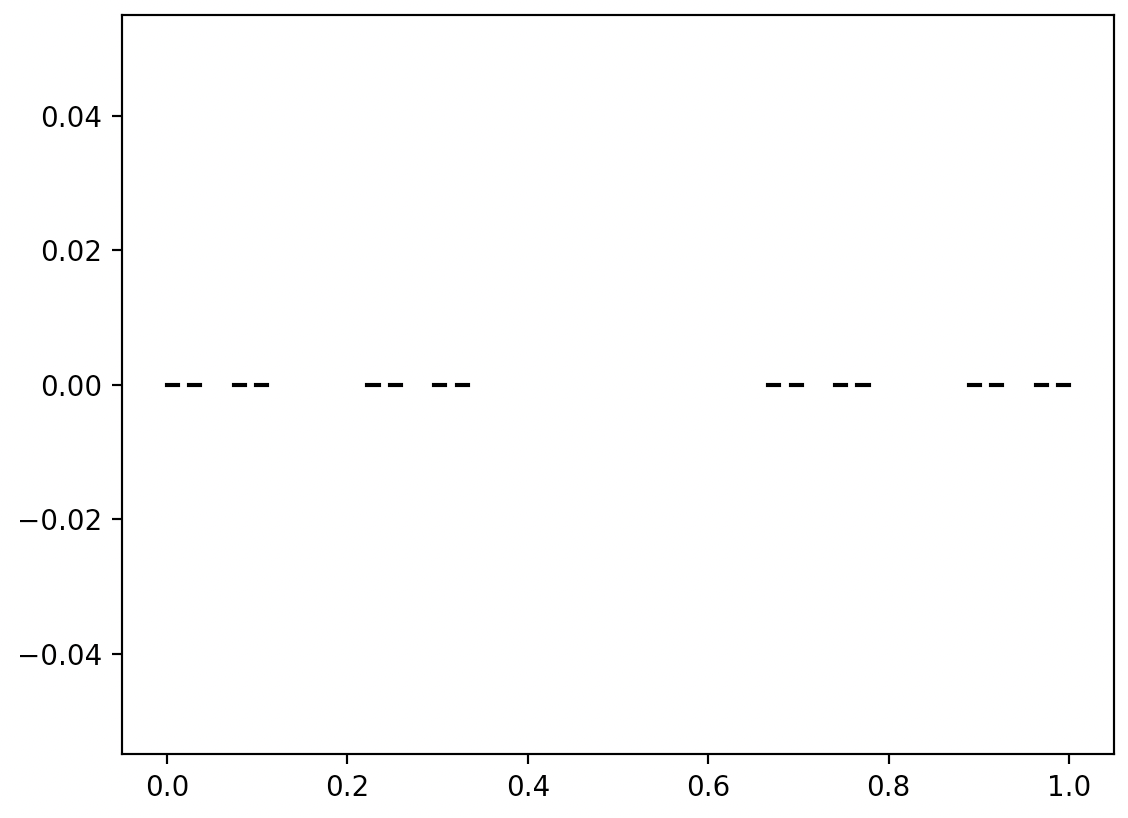

Wynik wykonania powyższych instrukcji

1.4.2 Trójkąt Sierpińskiego

Czas na kultowy trójkąt. Aby go narysować, wykorzystamy rekurencyjną funkcję sierpinski, która przyjmuje trzy argumenty: x – miejsce, od którego należy rysować fraktal, scale – informacje o wielkości fraktala oraz depth – aktualny poziom zagnieżdżenia fraktala.

# Wczytujemy niezbędne biblioteki.
import matplotlib.pyplot as plt
import numpy as np
import math

# Definiujemy funkcję rysującą trójkąt zaczepiony 
# w punkcie x o boku scale.
def triangle(x, scale): 
    plt.fill([x[0], x[0]+scale, x[0]+scale/2], 
        [x[1], x[1], x[1]+scale*np.sqrt(3)/2], 
        color = "black")
        
# Rekurencyjna funkcja do rysowania trójkąta Sierpińskiego. 
# Jeżeli depth=1, to rysujemy zwykły trójkąt, jeżeli depth>1, 
# to rysujemy trzy trójkąty obok siebie.        
def sierpinski(x, scale, depth):  
    if depth > 1: 
        sierpinski(x, scale/2, depth-1)
        sierpinski(np.add(x, [scale/2, 0]), 
            scale/2, depth-1)
        sierpinski(np.add(x,[scale/4,scale*np.sqrt(3)/4]), 
            scale/2, depth-1)
    else:
        triangle(x, scale)
        
# Inicjacja rysunku i narysowanie trójkąta o głębokości 4.
plt.figure() 
sierpinski([0,0], scale = 1, depth = 4)
plt.show()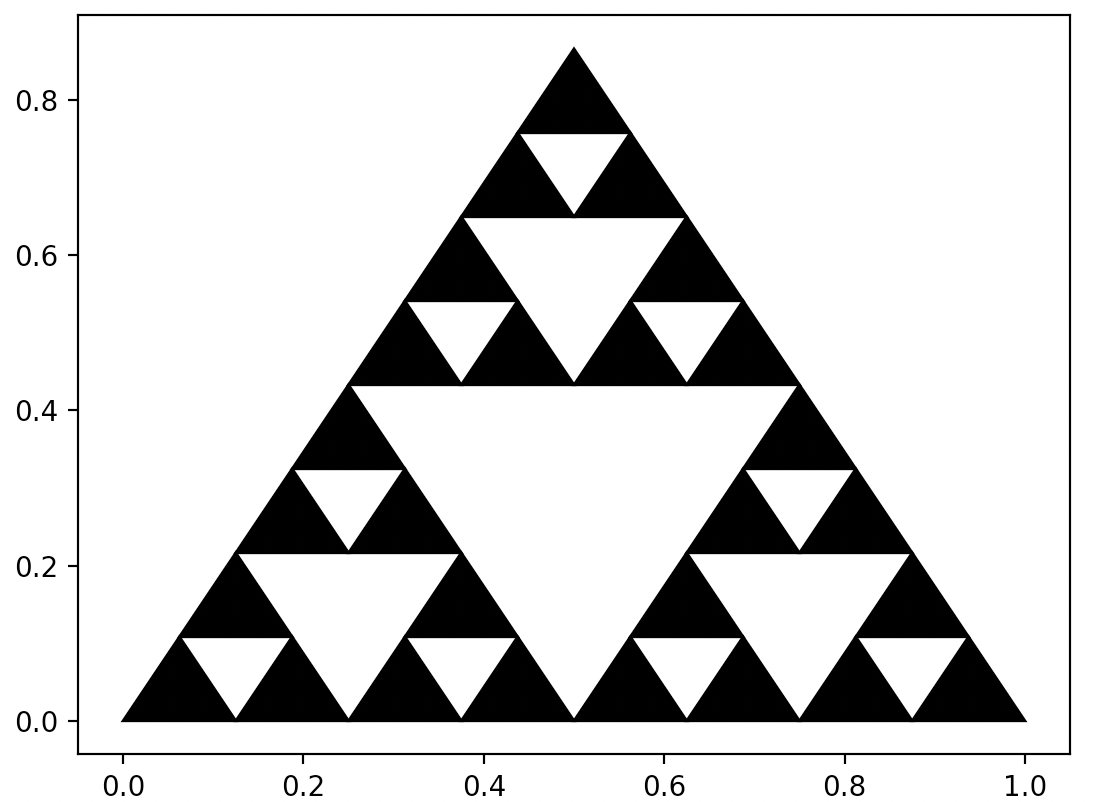

Wynik wykonania powyższych instrukcji

1.4.3 Dywan Sierpińskiego

Konstrukcja fraktala zaproponowana przez Wacława Sierpińskiego może być powtórzona dla innych kształtów, np. dla kwadratu lub pięciokąta.
Poniżej przykład dla kwadratu z dziurką, czyli dywanu Sierpińskiego.

import matplotlib.pyplot as plt
import numpy as np

# Rekurencyjna funkcja do rysowania dywanu Sierpińskiego. 
# Jeżeli depth=1, to rysujemy kwadrat, używając funkcji square(),
# jeżeli depth>1, to rysujemy osiem fraktali obok siebie. 
def square(x, scale):
    plt.fill(np.add(x[0], [0, scale, scale, 0]), 
        np.add(x[1], [0 0, scale,scale]), color="black")
def carpet(x, scale, depth):
    if depth > 1: 
        carpet(x, scale/3, depth-1)
        carpet(np.add(x, [scale/3,0]), scale/3,depth-1)
        carpet(np.add(x, [2*scale/3,0]), scale/3,depth-1)
        carpet(np.add(x, [0,scale/3]), scale/3,depth-1)
        carpet(np.add(x, [2*scale/3,scale/3]), scale/3,depth-1)
        carpet(np.add(x, [0,2*scale/3]), scale/3,depth-1)
        carpet(np.add(x, [scale/3,2*scale/3]), scale/3,depth-1)
        carpet(np.add(x, [2*scale/3,2*scale/3]), scale/3,depth-1)
    else:
        square(x, scale)
        
plt.figure()
carpet([0,0], scale = 1, depth = 4)
plt.show()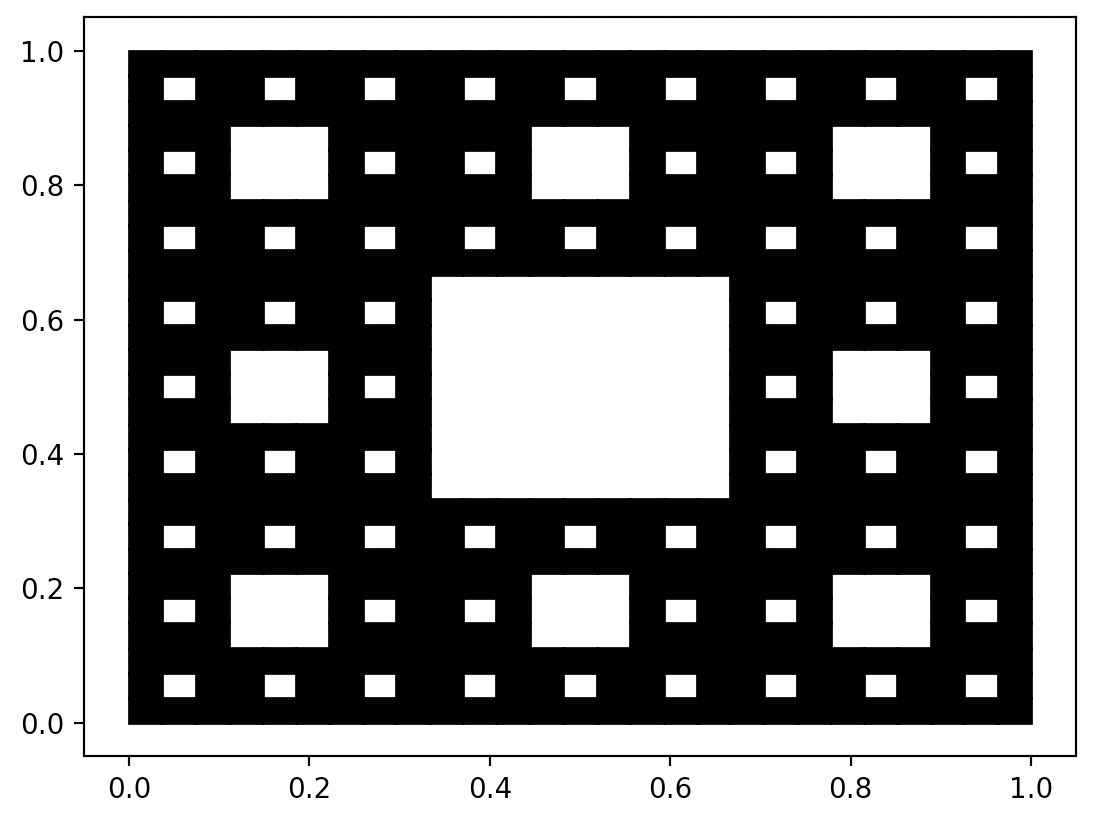

Wynik wykonania powyższych instrukcji