2.2 Fraktal, czyli punkt stały
Gwoździem programu będzie w tym rozdziale twierdzenie Banacha o punkcie stałym i związek tego twierdzenia z fraktalami. Zaczniemy od pokazania konstrukcji kilku nowych ciekawych figur, takich jak smok Heighwaya czy paproć Barnsleya. Zaspokoiwszy pierwszą ciekawość, zagłębimy się w podstawy matematyczne tych figur.
Dla osób, które studiowały matematykę, może to być przypomnienie pewnych pojęć z analizy matematycznej czy topologii. Dla osób, które matematyki nie studiowały, może to być interesujące spojrzenie na to, jak matematycy formułują tezy.
2.2.1 Smoki i paprocie
Pierwszy rozdział zostawił nas z metodą konstrukcji trzech fraktali. Każdy z nich można było wykonać przez powtarzanie w kółko następujących kroków.
Algorytm konstrukcji prostych fraktali.
- Weź jakąś figurę.
- Skopiuj ją \(x\) razy.
- Pomniejsz ją \(y\)-krotnie.
- Pomniejszone kopie poprzesuwaj.
- Wróć do kroku 2.
W przypadku kurzu Kantora kopiowaliśmy \(x=2\) razy, a pomniejszaliśmy \(y=3\) razy. Dla trójkąta Sierpińskiego kopiowaliśmy \(x=3\) razy, a pomniejszaliśmy \(y=2\) razy. Dla dywanu Sierpińskiego kopiowaliśmy \(x=8\) razy, a pomniejszaliśmy \(y=3\) razy.
Okazuje się, że w bardzo podobny sposób można stworzyć więcej różnych fraktali. A jeżeli obok skalowania i przesuwania pozwolimy jeszcze na obroty, to otrzymamy bardzo bogatą klasę różnorodnych ciekawych figur. Złożenie skalowania, przesuwania i obrotu jest na tyle ważną operacją, że doczekało się własnej nazwy: przekształcenie afiniczne.
W kroku 1 powyższego algorytmu wybieramy dowolną figurę. Ale im więcej razy powtarzamy krok 3 tego algorytmu, tym mniejsze są wybrane figury. W rzeczywistości wybór tej figury nie ma znaczenia, równie dobrze możemy na początku wykorzystać rysunek trójkąta czy słonia, czy małej kropki. Jak to możliwe? To będzie główny wniosek z twierdzenia Banacha o punkcie stałym.

Weźmy słonia i zróbmy z niego uszczelkę. Po sześciu iteracjach słoń i tak robi się wielkości ziarenka piasku
Ale najpierw poznajmy trzy nowe fraktale.
2.2.2 Pięciokąt Sierpińskiego (ang. Sierpiński pentagon)
Sztuczkę z trójkątem czy kwadratem możemy powtórzyć z każdym wielokątem foremnym, np. pięciokątem. Jeżeli będziemy wyjściową figurę kopiować pięciokrotnie, następnie zmniejszać ją o \(\frac{3-\sqrt 5}2 \approx 0,382\), a następnie przesuwać w rogi pięciokąta, tak by zmniejszone figury stykały się wierzchołkami, to powtarzając tę procedurę wielokrotnie, uzyskamy figurę nazywaną pięciokątem Sierpińskiego.

Pięciokąt Sierpińskiego. Wynik pięciokrotnego kopiowania wejściowej figury, pomniejszania i przesuwania tych kopii. Każdą z pięciu kopii oznaczono innym kolorem
Ale prawdziwa magia zaczyna się, gdy w tych transformacjach pozwolimy na obroty. Rozważmy poniższy algorytm.
Algorytm konstrukcji złożonych fraktali.
- Weź jakąś figurę.
- Skopiuj ją \(x\) razy.
- Pomniejsz ją \(y\)-krotnie.
- Pomniejszone kopie obróć i/lub przesuń.
- Idź do kroku 2.
Zobaczmy, jak ten algorytm działa na przykładzie kilku ciekawych zestawów transformacji.
2.2.3 Drzewo Pitagorasa
Konstrukcja tego fraktala została opisana w 1942 roku przez Alberta Bosmana. Jest kilka różnych wariantów budowy tej figury, poniżej przedstawiamy konstrukcję opartą na dwóch transformacjach.
- Transformacja 1: obróć figurę o \(45^{\circ}\) w lewo, a następnie przeskaluj ją współczynnikiem \(1/\sqrt{2}\).
- Transformacja 2: obróć figurę o \(45^{\circ}\) w prawo, a następnie przeskaluj ją współczynnikiem \(1/\sqrt{2}\).
Poniższy obrazek ilustruje fraktal oraz przedstawia samopodobieństwo wynikające ze składanych transformacji. Kod pozwalający na odtworzenie tego fraktala znajduje się na końcu rozdziału.
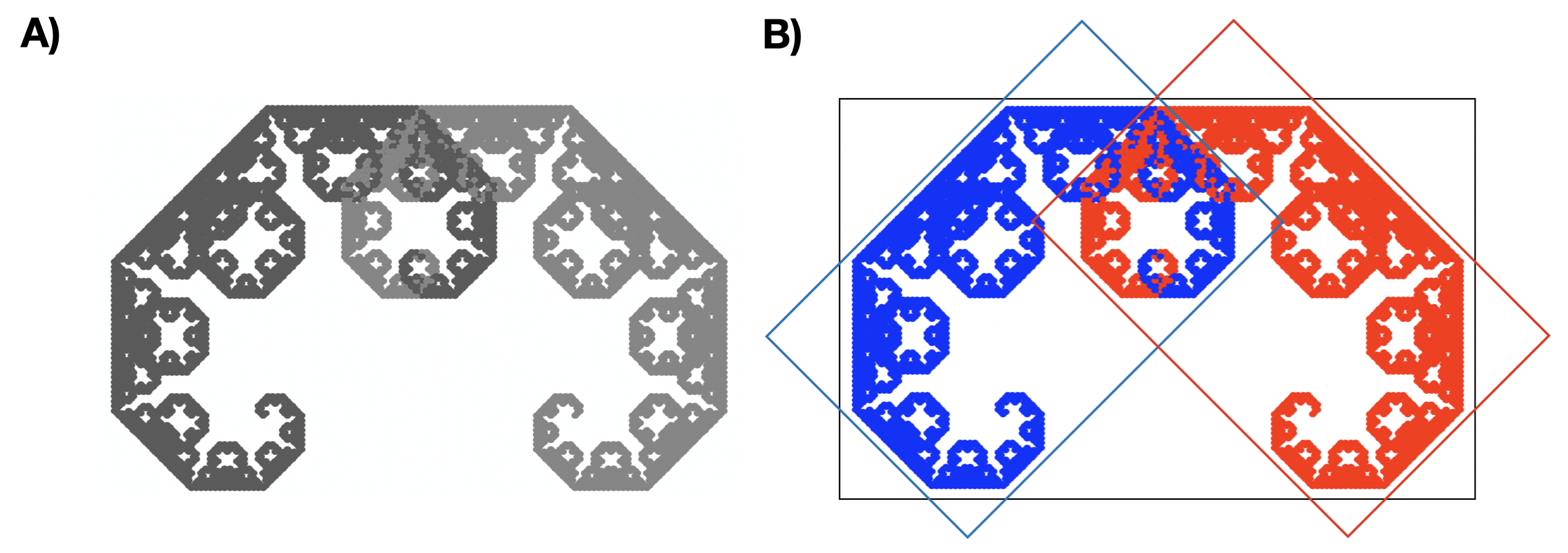
Panel A przedstawia drzewo Pitagorasa, panel B ilustruje dwie transformacje składające się na fraktal. Obraz jest zmniejszany sqrt(2) razy i obracany o 45 stopni, każdą z dwóch replikacji oznaczono innym kolorem
2.2.4 Smok Heighwaya
Okazuje się, że bardzo wiele ciekawych figur można uzyskać dwiema transformacjami. Jedną z nich jest smok Heighwaya, którego konstrukcję pokazali po raz pierwszy John Heighway, Bruce Banks i William Harter z NASA. Smok jest oparty na takich dwóch transformacjach:
- Transformacja 1: obróć figurę o \(45^{\circ}\) w lewo, a następnie przeskaluj ją współczynnikiem \(1/\sqrt 2\).
- Transformacja 2: obróć figurę o \(45^{\circ}\) w lewo, a następnie przeskaluj ją współczynnikiem \(1/\sqrt 2\) i przesuń o 1 wzdłuż osi poziomej.
Poniższy obrazek ilustruje smoka i obie transformacje. Kod pozwalający na odtworzenie tego fraktala znajduje się na końcu rozdziału.
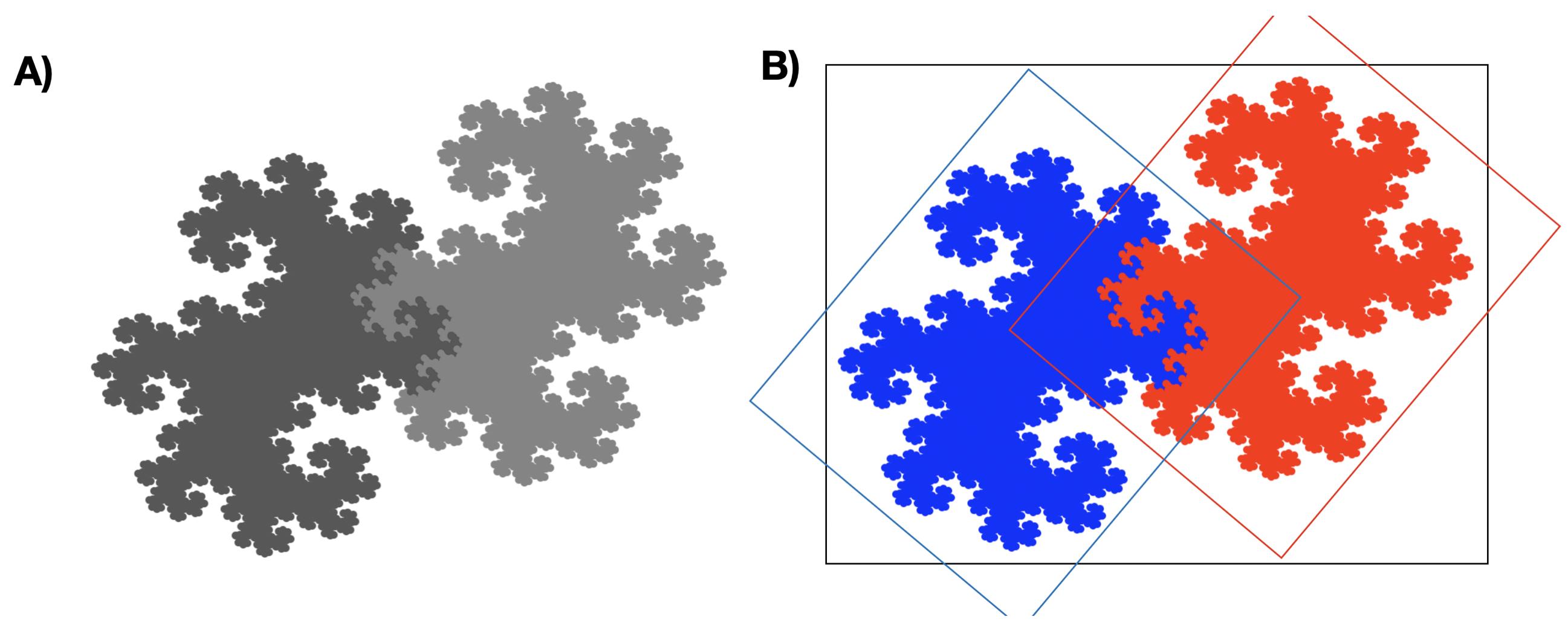
Panel A przedstawia smoka Heighwaya, panel B ilustruje dwie transformacje składające się na fraktal. Każdą z dwóch replikacji oznaczono innym kolorem
2.2.5 Paproć Bernseya
Dwiema transformacjami można uzyskać bardzo wiele, a co się stanie, gdy dodamy kolejne? Zobaczmy na przykładzie jednego z najpopularniejszych fraktali – paproci Barnsleya. Została ona po raz pierwszy opisana w 1993 roku przez brytyjskiego matematyka Michaela Barnsleya, który badał fraktale ze względu na ich potencjał we fraktalnej kompresji.
Do paproci będziemy potrzebowali potrzebowali czterech transformacji:
- Transformacja 1 (lewy liść): obróć figurę o \(10^{\circ}\) w lewo, a następnie przeskaluj ją współczynnikiem \((0,5; 0,3)\).
- Transformacja 2 (prawy liść): obróć figurę o \(15^{\circ}\) w prawo, a następnie przeskaluj ją współczynnikiem \((0,45; 0,25)\).
- Transformacja 3 (góra): obróć figurę o \(1^{\circ}\) w prawo, a następnie przeskaluj ją współczynnikiem \(0,9\) i przesuń o \(0,01\) wzdłuż osi X.
- Transformacja 4 (łodyga): przeskaluj figurę współczynnikiem \((0,25; 0)\).
Poniższy obrazek ilustruje paproć i wszystkie cztery transformacje. Kod pozwalający na odtworzenie tego fraktala znajduje się na końcu rozdziału.
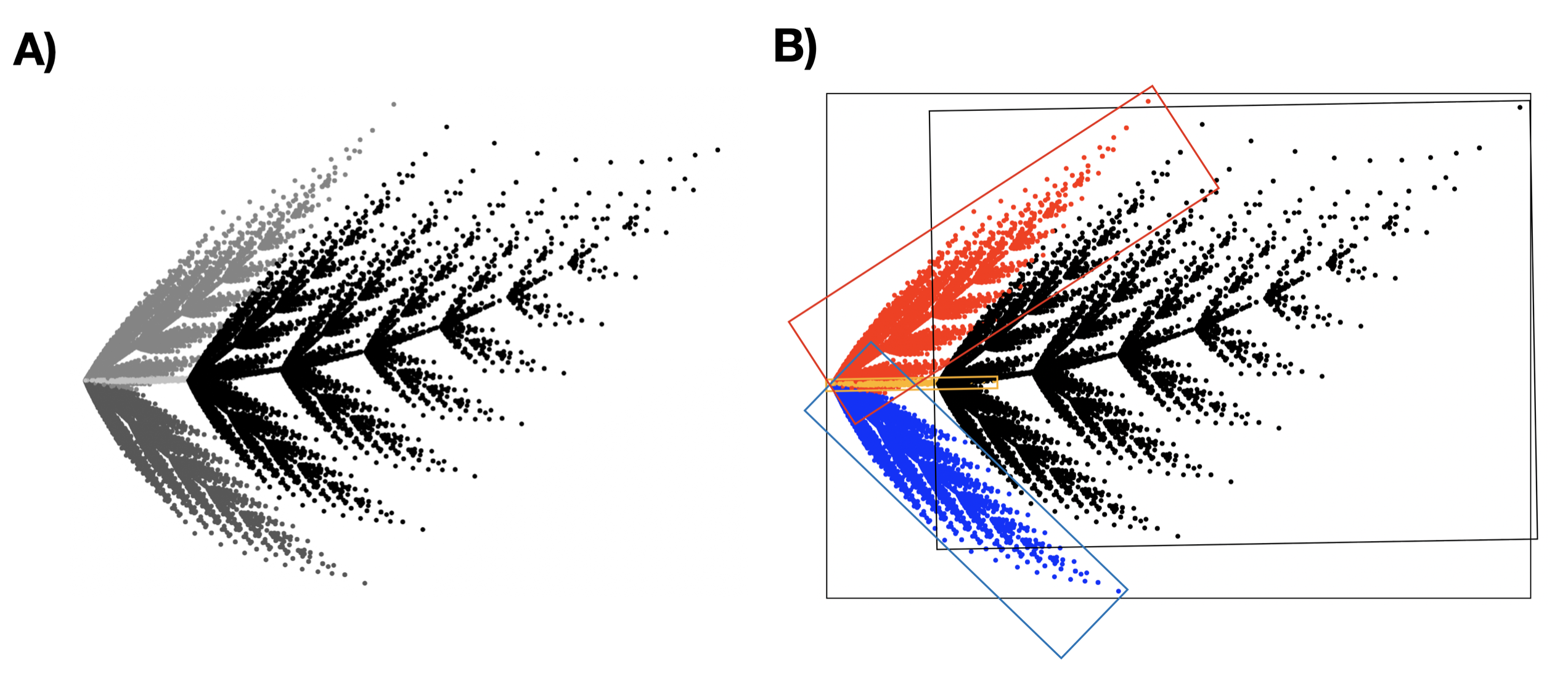
Panel A przedstawia paproć Barnsleya, panel B ilustruje cztery transformacje składające się na fraktal. Każdą z czterech replikacji oznaczono innym kolorem