2.3 Ale dlaczego to działa?
Pokazane figury mają bardzo ciekawy opis matematyczny. Przedstawiamy go poniżej na poziomie szczegółowości pierwszych lat studiów matematycznych. Najpierw zdefiniujemy kilka niezbędnych pojęć, w oparciu o które będziemy mogli przedstawić twierdzenie o punkcie stałym.
Zazwyczaj, myśląc o figurach i odległościach, skupiamy się na bardzo klasycznej płaszczyźnie z dwiema osiami i zwykłą euklidesową odległością. Ale na potrzeby zbliżającego się twierdzenia musimy spojrzeć na pewne rzeczy nieco bardziej abstrakcyjnie.
2.3.1 Przestrzeń metryczna
W naszej historii bardzo ważną rolę będą odgrywały odległości pomiędzy punktami. Dlatego w dalszej części tego rozdziału często będziemy pisać o przestrzeni metrycznej. Co to takiego?
Definicja (przestrzeń metryczna). Przestrzeń metryczna to zbiór \(X\) z określoną metryką (odległością) \(d\) pomiędzy punktami tego zbioru.
Inaczej mówiąc, jeżeli pracujemy z przestrzenią metryczną, to dla każdej pary punktów \(a\) i \(b\) potrafimy wyznaczyć ich odległość \(d(a,b)\).
Definicja (odległość). Odległość to funkcja \(d(a,b)\) określona dla każdych dwóch punktów \(a, b \in X\) spełniająca jednocześnie trzy warunki:
- \(d(a,b) = 0 \Leftrightarrow a = b\), odległość wynosi zero wtedy i tylko wtedy, gdy punkty są sobie równe,
- \(d(a,b) = d(b,a)\), odległość jest symetryczna,
- \(d(a,b) \leq d(a,c) + d(c,b)\), warunek trójkąta, czyli odległość pomiędzy dowolnymi dwoma punktami jest zawsze mniejsza lub równa niż suma odległości tych punktów od dowolnego innego punktu \(c\).
Większość z nas w codziennym życiu operuje w przestrzeni euklidesowej, ze zwykłą ,,linijkową’’ odległością. Ale aby pracować z fraktalami, potrzebujemy bardziej wyrafinowanych linijek.
2.3.2 Odległość Hausdorffa
W świecie fraktali odległość pomiędzy punktami mierzy się bardzo przewrotnie – stosując odległość Hausdorffa. Ta odległość określa, jak daleko od siebie są dwie figury (w sensie: zbiory punktów).
Mamy dwa zbiory punktów A i B w przestrzeni metrycznej z metryką \(d\) i chcemy określić, jak daleko od siebie są te zbiory. Intuicja stojąca za tą metryką jest następująca: zbiory są blisko siebie, jeżeli dla każdego punktu z jednego zbioru można znaleźć jakiś punkt z drugiego zbioru, który jest do niego bliski. Jeżeli każdy punkt ze zbioru \(A\) ma takiego ,,towarzysza’’ ze zbioru \(B\), to są one blisko.
Spróbujmy to zapisać formalnie.
Definicja (odległość Hausdorffa). Odległość Hausdorffa pomiędzy dwoma niepustymi zbiorami \(A\) i \(B\) określona jest jako
\[ d_H(A, B) = \max \left\{ \sup_{a\in A} \inf_{b\in B} d(a, b); \sup_{b \in B} \inf_{a \in A} d(a, b) \right\}. \]
Technicznie rzecz biorąc, odległość Hausdorffa jest określona dla zwartych niepustych zbiorów. Można ją stosować też dla zbiorów domkniętych, ale wtedy może przyjmować wartości nieskończone. My będziemy pracować na zbiorach zwartych, ale można nie mówić tego na głos i pewnie wiele osób nawet nie zauważy różnicy.
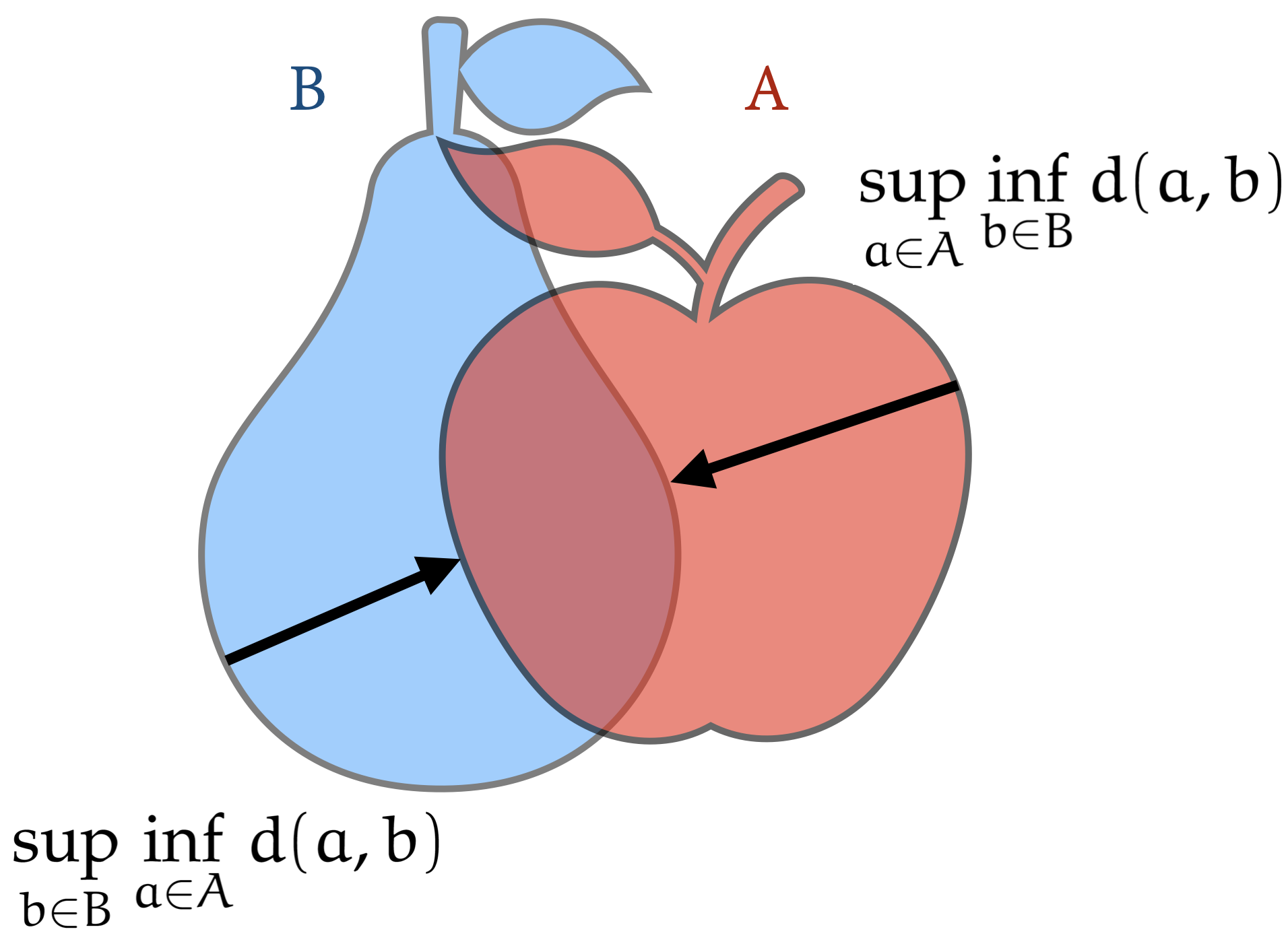
Ilustracja odległości Hausdorffa
Zapis może przerazić, ale jeżeli rozłożyć go na części, to okaże się bardzo intuicyjny. Cześć \(\inf_{b\in B} d(a, b)\) oznacza najmniejszą odległość od punktu \(a\) do dowolnego punktu ze zbioru \(B\). W takim razie \(\sup_{a\in A} \inf_{b\in B} d(a, b)\) to odległość najbardziej odstającego punktu ze zbioru \(A\). Odległość musi być symetryczna, więc we wzorze \(d_H(A, B)\) mamy maksimum z odstawiania zbioru \(A\) od \(B\) i odwrotnie.
2.3.3 Ciąg Cauchy’ego
Drogi Czytelniku, jak już pewnie zauważyłeś, konstruując fraktale, powtarzamy pewne czynności w kółko. Tu i tam pojawia się sugestia, że należy to robić w nieskończoność. Zabawa w nieskończoność jest jednak ryzykowna, szczególnie, jeżeli nie mamy gwarancji, że gdzieś zbiegniemy. Skąd wziąć te gwarancje?
Definicja (ciąg Cauchy’ego). Ciąg Cauchy’ego to ciąg punktów \(a_n\), w którym dla dowolnej większej od zera liczby \(\varepsilon\) można znaleźć taki element ciągu \(N\), że odległość pomiędzy wszystkimi dalszymi elementami jest mniejsza od \(\varepsilon\).
\[ \forall_{\varepsilon >0} \exists_N \forall_{m,n>N} d(a_m,a_n) \leq \varepsilon. \]
2.3.4 Przestrzeń zupełna
Ciągi zbieżne spełniają warunek Cauchy’ego, ale są też takie przestrzenie, w których ciągi Cauchy’ego nie są zbieżne. To nie są porządne przestrzenie, więc dalej będziemy operować tylko na porządnych przestrzeniach, czyli przestrzeniach zupełnych.
Definicja (przestrzeń zupełna). Przestrzeń metryczna \((X,d)\) jest zupełna, jeżeli każdy ciąg \(a_n \subset X\) spełniający warunek Cauchy’ego jest zbieżny w \(X\).
I to są właśnie gwarancje ,,porządności’’, których potrzebowaliśmy.
2.3.5 Kontrakcja
Mamy porządną przestrzeń, teraz porozmawiajmy o transformacjach. Do konstrukcji fraktali możemy wykorzystywać specyficzne transformacje, które zbliżają punkty. Będziemy je nazywać przekształceniami zwężającymi lub w skrócie kontrakcjami.
Definicja (kontrakcja). Przekształcenie \(T\) jest przekształceniem zwężającym (kontrakcją), jeżeli istnieje stała \(\lambda < 1\) taka, że
\[ \forall_{x,y} d(T(x), T(y)) \leq \lambda d(x,y). \]
Czyli dla dowolnych dwóch punktów \(x\) i \(y\) po przekształceniu są one bliżej niż przed.
W przykładach, o których rozmawialiśmy na początku rozdziału, każda pokazana transformacja była kontrakcją. Dlaczego? Transformacje składały się z obrotów, przesunięć i skalowania. Obrót i przesunięcie nie zmieniają odległości pomiędzy punktami, a wszystkie skalowania były wykonywane ze skalą mniejszą niż 1 dla każdej z osi.
2.3.6 Przekształcenie afiniczne
Kontrakcje to bardzo szeroka klasa transformacji. My ograniczamy się do znacznie węższej klasy transformacji liniowych z przesunięciami, czyli tzw. przekształceń afinicznych.
Przekształcenie afiniczne to złożenie skalowania, obrotu i przesunięcia.
Jeżeli skalowanie zmniejsza figurę, to takie przekształcenie afiniczne jest kontrakcją, ponieważ obrót i przesunięcie nie zmienia odległości.
Przekształcenia afiniczne można łatwo opisać w postaci algebraicznej jako mnożenie punktu przez macierz przekształcenia. Pozwoli nam to skrócić zapis kodu generującego fraktal:
\[ T_{rotate, \alpha}(x) = \begin{bmatrix} \cos(\alpha) & -\sin(\alpha) \\ \sin(\alpha) & \cos(\alpha) \end{bmatrix} x, \]
\[ T_{scale, a, b}(x) = \begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} x, \]
\[ T_{shift, a, b}(x) = x + \begin{bmatrix} a \\ b \end{bmatrix}. \]
2.3.7 Twierdzenie Hutchinsona
W tym miejscu ktoś powie: ,,OK, każda z transformacji jest kontrakcją, ale czy ich złożenie też musi być kontrakcją?’’. Konstruując trójkąt Sierpińskiego, co prawda pomniejszaliśmy figurę, ale później kopiowaliśmy ją trzy razy. Okazuje się, że suma kontrakcji też jest kontrakcją – i dokładnie o tym mówi twierdzenie Hutchinsona.
Twierdzenie Hutchinsona. Przekształcenie \(T = T_1 \cup T_2 \cup ... \cup T_k\) jest zwężające, jeśli wszystkie przekształcenia \(T_1, ..., T_k\) użyte do zdefiniowania przekształcenia \(T\) są zwężające.
Dowód tego twierdzenia nie jest długi, można go znaleźć np. w ,,Delcie’’ z lipca 2011 roku [Kici11].
2.3.8 Twierdzenie Banacha o punkcie stałym
Mamy już wszystko, czego potrzebowaliśmy do pokazania twierdzenia Banacha o punkcie stałym, czyli porządną przestrzeń z porządną odległością, w której używamy operatora \(T\), który jest kontrakcją. Precyzyjniej:
Twierdzenie Banacha o punkcie stałym. Jeśli \((X, d)\) jest przestrzenią metryczną zupełną, a \(T: X\to X\) jest kontrakcją, to \(T\) ma dokładnie jeden punkt stały \(x\in X\).
Puntem stałym przekształcenia \(T\) jest taki punkt \(x\), że \(T(x) = x\).
Dowód tego twierdzenia Banach przedstawił w swojej pracy doktorskiej. Nie jest on zbyt skomplikowany, można go znaleźć np. w ,,Delcie’’ z lipca 2011 roku. Tutaj ograniczymy się jedynie do pokazania, jak szukać tego punktu stałego.
Otóż okazuje się, że dla dowolnego punktu \(x\) przestrzeni \(X\) ciąg \(T^n(x)\) zbiega do punktu stałego, gdzie \(T^n(x)\) oznacza n-krotne złożenie przekształcenia \(T\), czyli \(T(T(T(...T(x)...)))\). Wystarczy zatem w nieskończoność składać kontrakcje, by znaleźć ich punkt stały.
I takim punktem stałym są konstruowane przez nas fraktale.