3.5 Przykłady w języku R
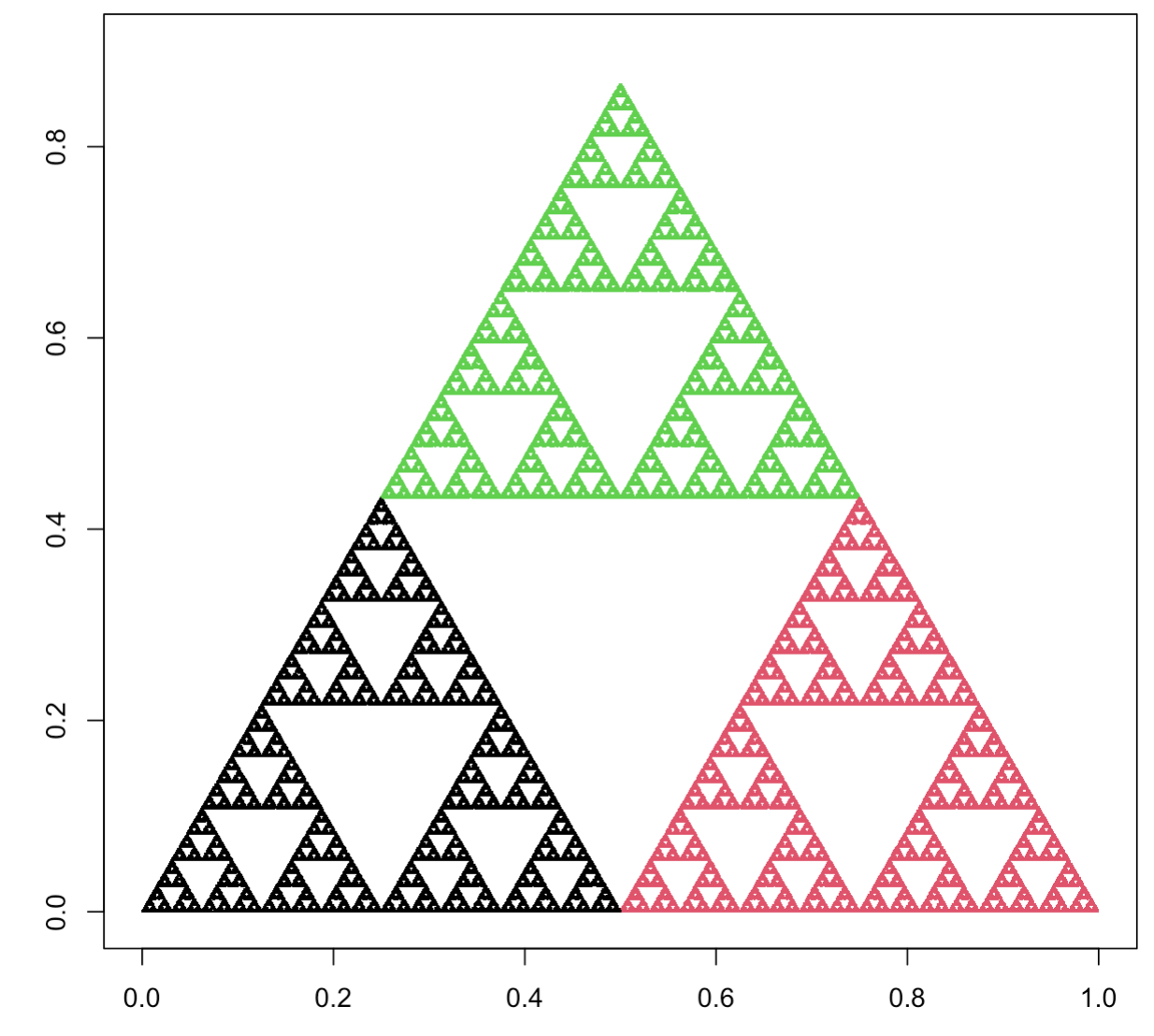
3.5.1 Trójkąt Sierpińskiego raz jeszcze
Poniższy kod odtwarza konstrukcję trójkąta Sierpińskiego przedstawioną w tym rozdziale. W wektorze triangle definiujemy trzy wierzchołki trójkąta, a w obiekcie point umieszczamy współrzędne punktu startowego dla konstrukcji fraktala. Następnie w pętli przesuwamy punkt w kierunku losowego wierzchołka.
- \(x' = x/2\), \(y' = y/2\) (lewy róg)
- \(x' = x/2 + \frac 12\), \(y' = y/2\) (prawy róg)
- \(x' = x/2 + \frac 14\), \(y' = y/2 + \frac{\sqrt{3}}2\) (górny róg)
N = 200000
x = y = 0
plot(0, xlim = c(0,1), ylim = c(0,0.9),
xlab = "", ylab = "", col="white", asp=1)
for (i in 1:N) {
# Trzy transformacje zapisujemy jako różne scenariusze w bloku instrukcji switch.
ind = sample(1:3, 1)
switch(ind,
'1' = {x <- x/2; y <- y/2},
'2' = {x <- x/2 + 1/2; y <- y/2},
'3' = {x <- x/2 + 1/4; y <- y/2 + sqrt(3)/4})
points(x, y, pch = ".", col=ind)
}
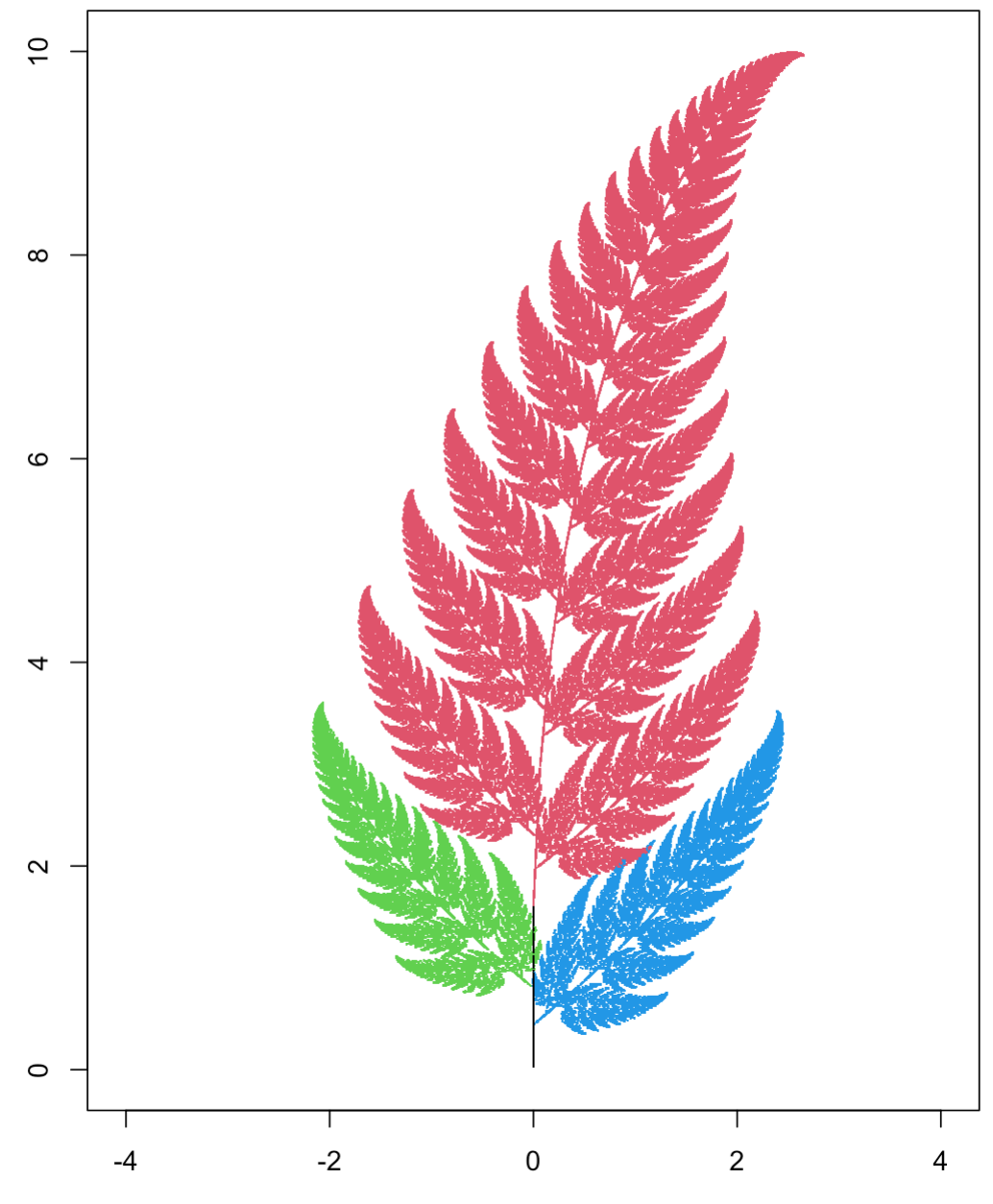
3.5.2 Paproć Barnsleya
trans1 = function(x,y)
c(0., 0.16*y)
trans2 = function(x,y)
c(0.85*x + 0.04*y, -0.04*x + 0.85*y + 1.6)
trans3 = function(x,y)
c(0.2*x - 0.26*y, 0.23*x + 0.22*y + 0.8)
trans4 = function(x,y)
c(-0.15*x + 0.28*y, 0.26*x + 0.24*y + 0.44)
# W tym przykładzie transformacje (które są funkcja)
# złożyliśmy w listę, aby łatwiej było na nich pracować.
trans = list(trans1, trans2, trans3, trans4)
probs = c(0.01, 0.79, 0.1, 0.1)
N = 200000
x = y = 0
plot(0, xlim = c(-2.5,2.5), ylim = c(0,10),
xlab = "", ylab = "", col="white", asp=1)
for (i in 1:N) {
ind = sample(seq_along(trans), 1, prob = probs)
res = trans[[ind]](x, y)
x = res[1]
y = res[2]
points(x, y, pch = ".", col=ind)
}
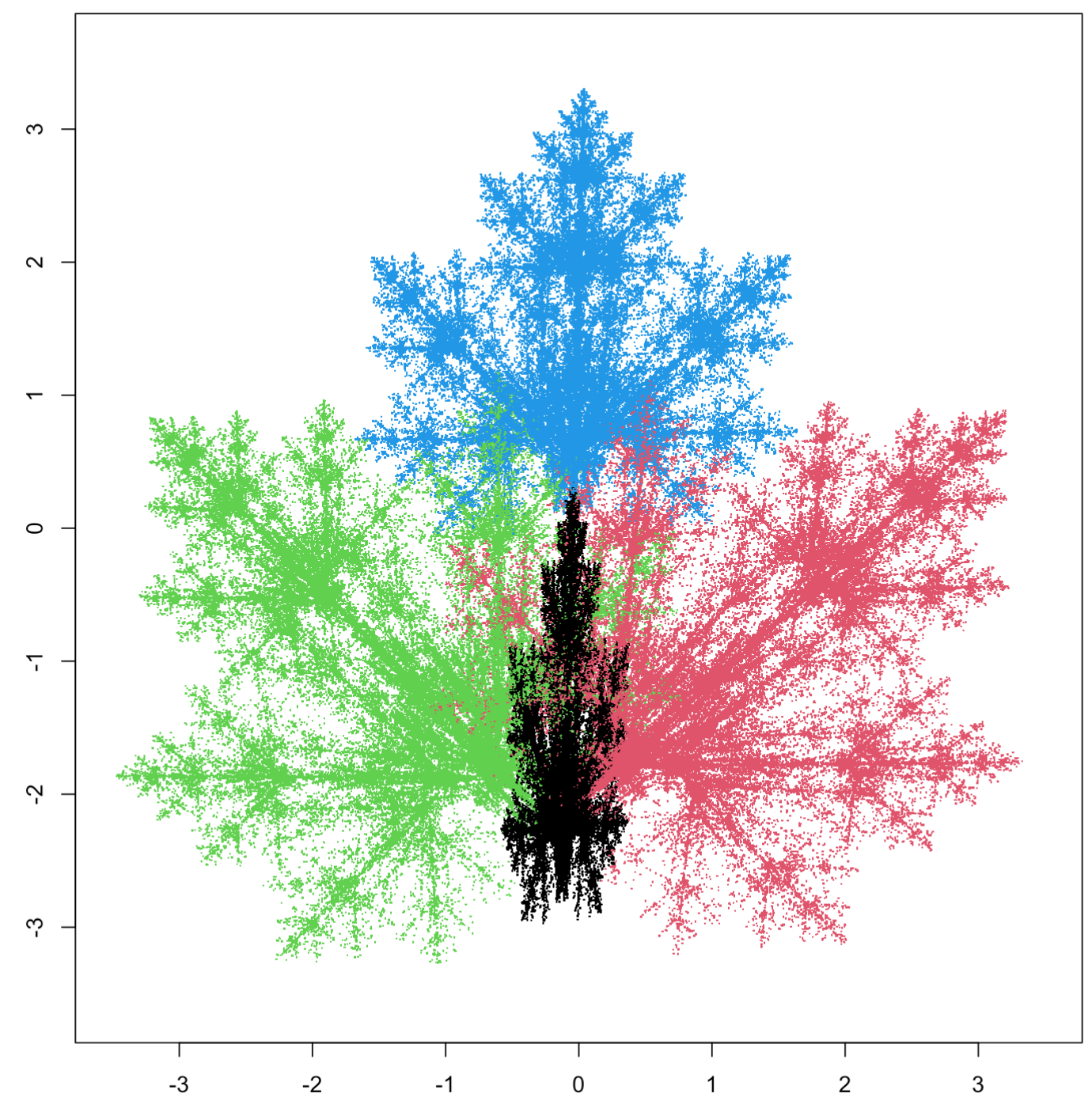
3.5.3 Liść klonu
transform = function(x,y, affine)
c(affine[1]*x + affine[2]*y + affine[3],
affine[4]*x + affine[5]*y + affine[6])
N = 400000
x = y = 0
# Lista transformacji, przechowujemy ją jako listę wektorów
# o długości 6.
affines = list(c(0.14, 0.01, -0.08, 0.0, 0.51, -1.31),
c(0.43, 0.52, 1.49, -0.45, 0.5, -0.75),
c(0.45, -0.49, -1.62, 0.47, 0.47, -0.74),
c(0.49, 0.0, 0.02, 0.0, 0.51, 1.62))
probs = c(0.25, 0.25, 0.25, 0.25)
plot(0, xlim = c(-3.5,3.5), ylim = c(-3.5,3.5),
xlab = "", ylab = "", col="white", asp=1)
for (i in 1:N) {
# Losujemy transformacje uwzględniając prawdopodobieństwa
# wskazane w wektorze probs
ind = sample(seq_along(affines), 1, prob = probs)
res = transform(x, y, affines[[ind]])
x = res[1]
y = res[2]
points(x, y, pch = ".", col=ind)
}