2.6 Przykłady w języku Julia
2.6.1 Trójkąt Sierpińskiego
Fraktale możemy budować ze zwykłych kropek, nie potrzebujemy bardziej wyrafinowanych figur. Poniższy przykład z kropek buduje trójkąt Sierpińskiego.
using Plots
# Poniższy program powtarza złożenie funkcji sierpinski
# depth razy. W teorii robilibyśmy to w nieskończoność,
# ale do uzyskania wyraźnego obrazka wystarczy kilka kroków.
# Liczba punktów rośnie wykładniczo, więc po k krokach wynosi 3^k.
function sierpinski(x, y, depth)
if depth > 1
sierpinski(x/2, y/2, depth-1)
sierpinski(x/2 + 0.5, y/2, depth-1)
sierpinski(x/2 + 0.25, y/2 + 0.5, depth-1)
else
scatter!([x], [y], color=:black,
legend=:false, markersize=2)
end
end
# Inicjacja pustego wykresu i narysowanie trójkąta Sierpińskiego.
plot(0, xlim=(-0.1,1.1), ylim=(-0.1,1.1), axis=nothing)
sierpinski(0, 0, 9)
Wynik wykonania powyższych instrukcji
2.6.2 Pięciokąt Sierpińskiego
# Rekurencyjnie rysujemy każde z ramion pięciokąta.
function pentagon(x, depth, col)
if depth > 1
x1 = 0.382x
x2 = 0.382x + [0.618 0]
x3 = 0.382x + [0.809 0.588]
x4 = 0.382x + [0.309 0.951]
x5 = 0.382x + [-0.191 0.588]
pentagon(x1, depth-1, "red")
pentagon(x2, depth-1, "blue")
pentagon(x3, depth-1, "green")
pentagon(x4, depth-1, "orange")
pentagon(x5, depth-1, "brown")
else
# Rysujemy jeden punkt po punkcie, przez co
# tworzenie fraktala jest czasochłonne.
# W kolejnym rozdziale zrobimy to lepiej.
scatter!([x[1]], [x[2]], color=col,
legend=:false, markersize=2)
end
end
plot(0, xlim=(-0.35,1.35), ylim=(-0.1,1.6), axis=nothing)
pentagon([0 0], 6, "black")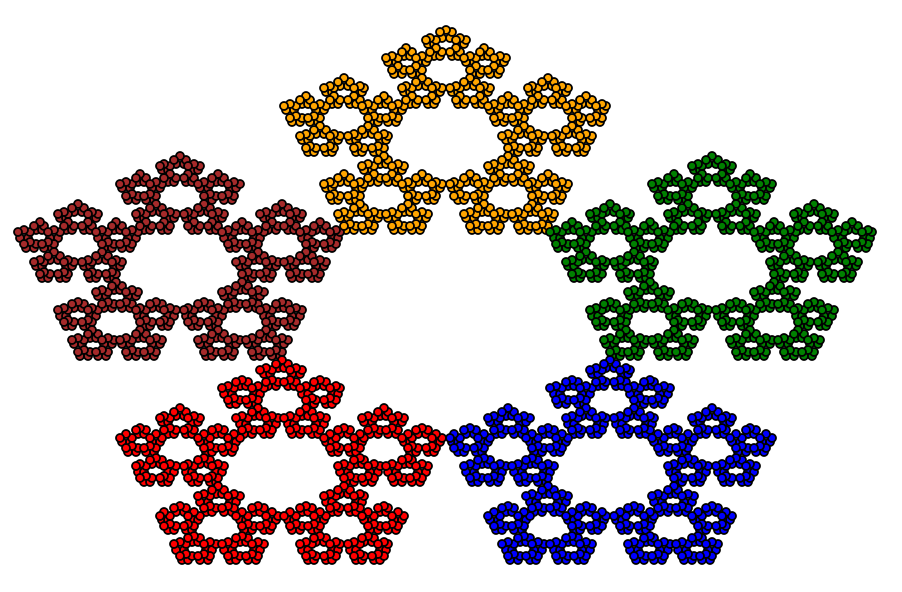
Wynik wykonania powyższych instrukcji
2.6.3 Smok Heighwaya
W języku Julia dodawanie i skalowanie macierzy wykonuje się używając standardowych operatorów. Potrzebujemy zdefiniować funkcję dla obrotu wektora x o kąt \(\alpha\).
# Obrót o kąt alpha (w stopniach).
function rotatex(x, alpha)
sa = sin(pi * alpha / 180)
ca = cos(pi * alpha / 180)
[ca -sa; sa ca] * x
end
# Symbol ' oznacza transpozycje macierzy.
# Potrzebujemy go by zamienić wektor wierszowy w kolumnowy.
function heighway(x, depth, col)
if depth > 1
x1 = rotatex(x, -45) * sqrt(0.5)
x2 = rotatex(x, -45) * sqrt(0.5) + [0.75 0.25]'
heighway(x1, depth-1, "blue")
heighway(x2, depth-1, "red")
else
scatter!([x[1]], [x[2]], color=col,
legend=:false, markersize=2)
end
end
plot(0, xlim=(-0.5,1.5), ylim=(-1,0.5), axis=nothing)
heighway([0 0]', 14, "black")
Wynik wykonania powyższych instrukcji
2.6.4 Drzewo Pitagorasa
# Konstrukcja drzewa Pitagorasa jest bardzo podobna do
# smoka Heighwaya. W ostatnim rozdziale pokażemy jak
# płynnie przejść od jednego do drugiego.
function sbt(x, depth, col)
if depth > 1
x1 = rotatex(x, -45) * 0.7 + [0 1]'
x2 = rotatex(x, 45) * 0.7 + [0 1]'
sbt(x1, depth-1, "blue")
sbt(x2, depth-1, "red")
else
scatter!([x[1]], [x[2]], color =col,
legend=:false, markersize = 2)
end
end
plot(0, xlim=(-2,2), ylim=(0.5,3), axis=nothing)
sbt([0 0]', 14, "black")
Wynik wykonania powyższych instrukcji