1.2 Witajcie, fraktale!

To fascynujące, że powtarzanie w nieskończoność tych samych czynności może prowadzić do powstania arcyciekawych figur – fraktali.

Taką figurę może narysować każdy, wystarczy podstawowa znajomość programowania. Krok po kroku pokażemy, jak skonstruować różne klasy fraktali. Znajomość podstaw algebry, prawdopodobieństwa lub topologii pozwala dokładniej zrozumieć, skąd się te zaskakujące figury biorą.

1.2.1 Kurz Cantora

Jedną z ciekawszych metod konstrukcji fraktali jest metoda ,,przez wygryzanie’’. Bierzemy pewną figurę, a następnie usuwamy z niej (wygryzamy) kawałki. To, co zostaje, jest fraktalem, często o zaskakujących właściwościach. Zilustrujmy to na przykładzie fraktala nazywanego kurzem Cantora (od nazwiska Georga Cantora, pioniera teorii mnogości).

Receptura na konstrukcję kurzu Cantora.

1. Weź odcinek o dowolnej długości (ale dla uproszczenia nasz będzie miał długość 1).
2. Podziel ten odcinek na trzy równe części.
3. Usuń wnętrze środkowej części, przez co otrzymasz dwa odcinki, oba o długości 1/3 wyjściowego odcinka.
4. Dla każdego z otrzymanych odcinków kontynuuj dzielenie, idąc do kroku 2.

Ilustracja pięciu kolejnych kroków algorytmu wygryzania znajduje się na Rysunku 1.

Rysunek 1: Pierwsze 5 iteracji w konstrukcji kurzu Cantora

Powyższy algorytm cechuje kilka elementów typowych dla fraktali. Po pierwsze, nigdy się nie kończy, całą procedurę należy (przynajmniej w teorii) powtarzać nieskończenie wiele razy. Po drugie, mamy do czynienia z rekurencją. Trzeci krok prowadzi do powstania zbioru dwóch obiektów, a następnie każdy z nich jest ponownie przekształcany w taki sam sposób jak obiekt wyjściowy.

Postępując bardzo podobnie, można otrzymać wiele ciekawych figur, ale przyjrzyjmy się jeszcze przez chwilę kurzowi Cantora. Zobaczmy, co my właściwie otrzymaliśmy w wyniku tej procedury.

Sprawdźmy może, jak duży jest ten obiekt, czyli jaką ma długość. Początkowo odcinek miał długość \(1\), ale w pierwszym kroku usunęliśmy \(1/3\). W drugim kroku usunęliśmy \(2\) razy po \((1/3)^2\). Powtarzając to kilkukrotnie, w kroku \(k\) usuwamy \(2^{k-1}\) odcinków, każdy o długości \((1/3)^k\). A więc długość tego tworu w kroku \(k\) to:

\[\begin{equation} \begin{split} 1 &- 1/3 - 2*(1/3)^2 - ... - 2^{k-1}*(1/3)^k = \\ & 1 - \sum_{i=1}^k 2^{i-1}*(1/3)^i = 1 - 1/2 \sum_{i=1}^k (2/3)^i = \\ & 1 - \frac 12 (2 - 2 (2/3^k)) = (2/3)^k \xrightarrow[k\rightarrow \infty]{} 0 \end{split} \end{equation}\]

Do tego samego wniosku można dojść, stosując inne rozumowanie, a mianowicie patrząc, ile zostało z odcinka po \(k\)-tym kroku. Po pierwszym kroku mamy \(2\) odcinki długości \(1/3\), po drugim kroku mamy \(2^2\) odcinków długości \((1/3)^2\), a po kroku \(k\) mamy \(2^k\) odcinków o długości \((1/3)^k\). Do czego zbiega ten ciąg?

\[ \lim_{k \rightarrow \infty} (2/3)^k = 0 \]

Nie ma więc wątpliwości. Zbiór Cantora ma długość równą \(0\). Ale ewidentnie nie jest zbiorem pustym, bo ma wiele punktów. Jak wiele? Okazuje się, że tyle samo co cały odcinek, a więc nieprzeliczalnie wiele. Pokażmy to za pomocą pewnego sprytnego dowodu.

Twierdzenie (liczność zbioru Cantora). Zbiór Cantora jest równoliczny z odcinkiem \([0, 1]\).

Dowód: Aby policzyć punkty w zbiorze Cantora, musimy dla każdego punktu skonstruować rodowód, a więc zapis pozwalający jednoznacznie zidentyfikować każdy punkt. Rodowodem jednoznacznie identyfikującym punkt nazwiemy zbiór decyzji określających, jak do tego punktu dotrzeć w kolejnych krokach procedury generującej kurz Cantora.

Pamiętamy, że w każdym kroku usuwane są środki z odcinków, więc punkt, który należy do kurzu Cantora, będzie leżał albo w lewym albo w prawym odcinku. Ten wybór (lewy/prawy) trzeba podjąć w każdym kroku konstrukcji kurzu. Taki rodowód możemy zapisać przez nieskończoną sekwencję cyfr 0/1 – jeżeli w sekwencji na pozycji \(k\) występuje 0, to punkt należy do lewego pododcinka, jeżeli 1, to do prawego.

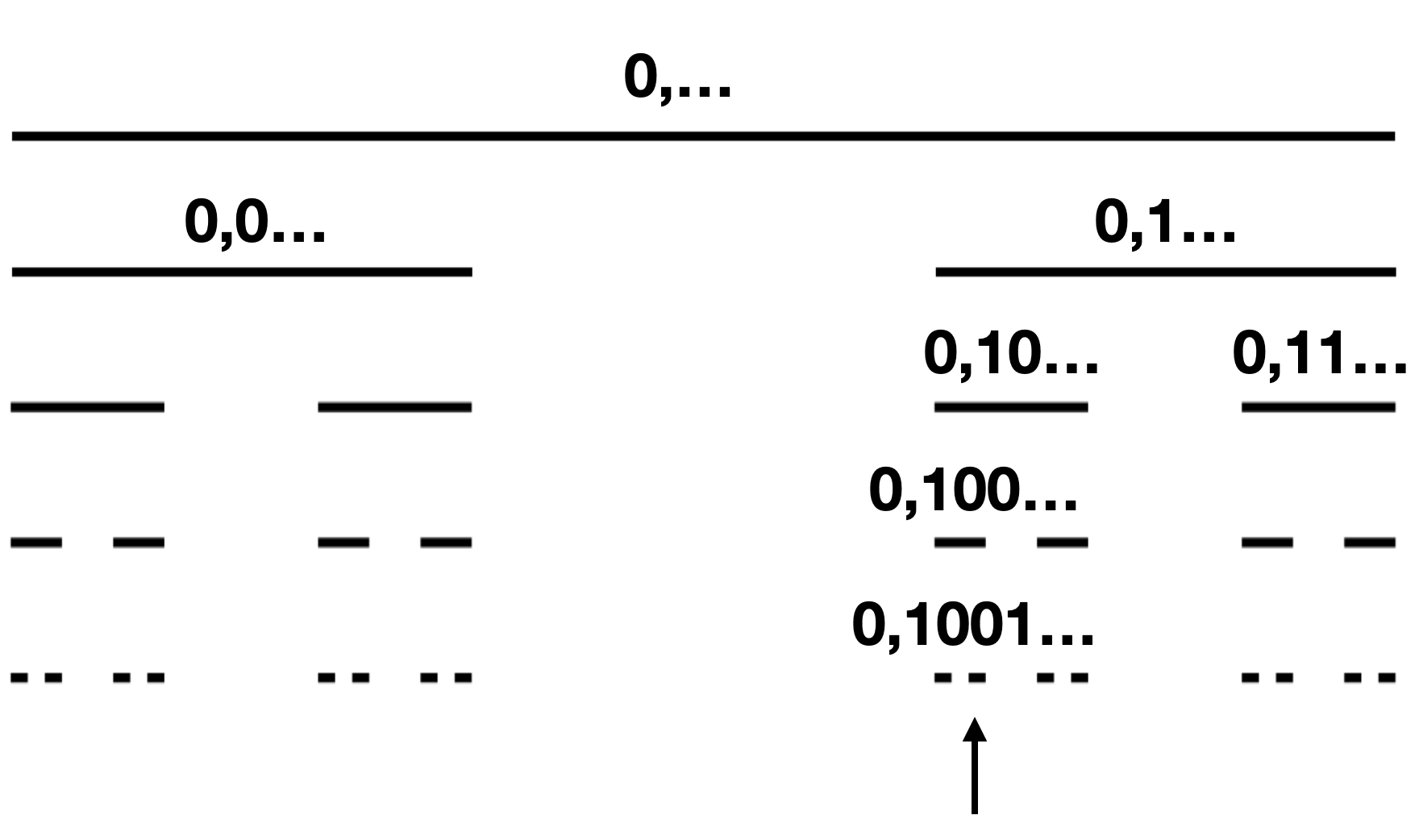
Zauważmy jednoznaczność -> każdy punkt z kurzu Cantora może być opisany przez nieskończoną sekwencję cyfr 0/1. Jednocześnie każda nieskończona sekwencja cyfr opisuje jakiś punkt ze zbioru Cantora, a różne sekwencje opisują różne punkty. Ile jest takich sekwencji? Tyle samo co w całym odcinku. Wystarczy bowiem myśleć o tych sekwencjach jak o rozwinięciach dwójkowych liczb z przedziału \([0, 1]\). ∎

Co więc mamy? Kurz Cantora ma tyle samo punktów co odcinek \([0, 1]\). Ale jednocześnie ma długość 0, choć odcinek ma oczywiście długość 1.

Jak to możliwe? To jedna z wielu zagadek kryjących się w krainie fraktali malowanych nieskończonością.

1.2.2 Trójkąt Sierpińskiego

Jeden z najbardziej znanych fraktali to z pewnością trójkąt Sierpińskiego, którego konstrukcja jest dosyć podobna do metody tworzenia kurzu Cantora.

Receptura na konstrukcję trójkąta Sierpińskiego.

1. Weź trójkąt równoboczny o dowolnej wielkości.
2. Podziel ten trójkąt na cztery trójkąty równoboczne.
3. Usuń wnętrze środkowego trójkąta, przez co otrzymasz trzy trójkąty z brzegiem, wszystkie o wielkości boku 1/2 wyjściowego trójkąta.
4. Dla każdego z trzech otrzymanych trójkątów kontynuuj dzielenie idąc do kroku 2.

Ilustracja czterech kolejnych kroków algorytmu wygryzania znajduje się na Rysunku 2.

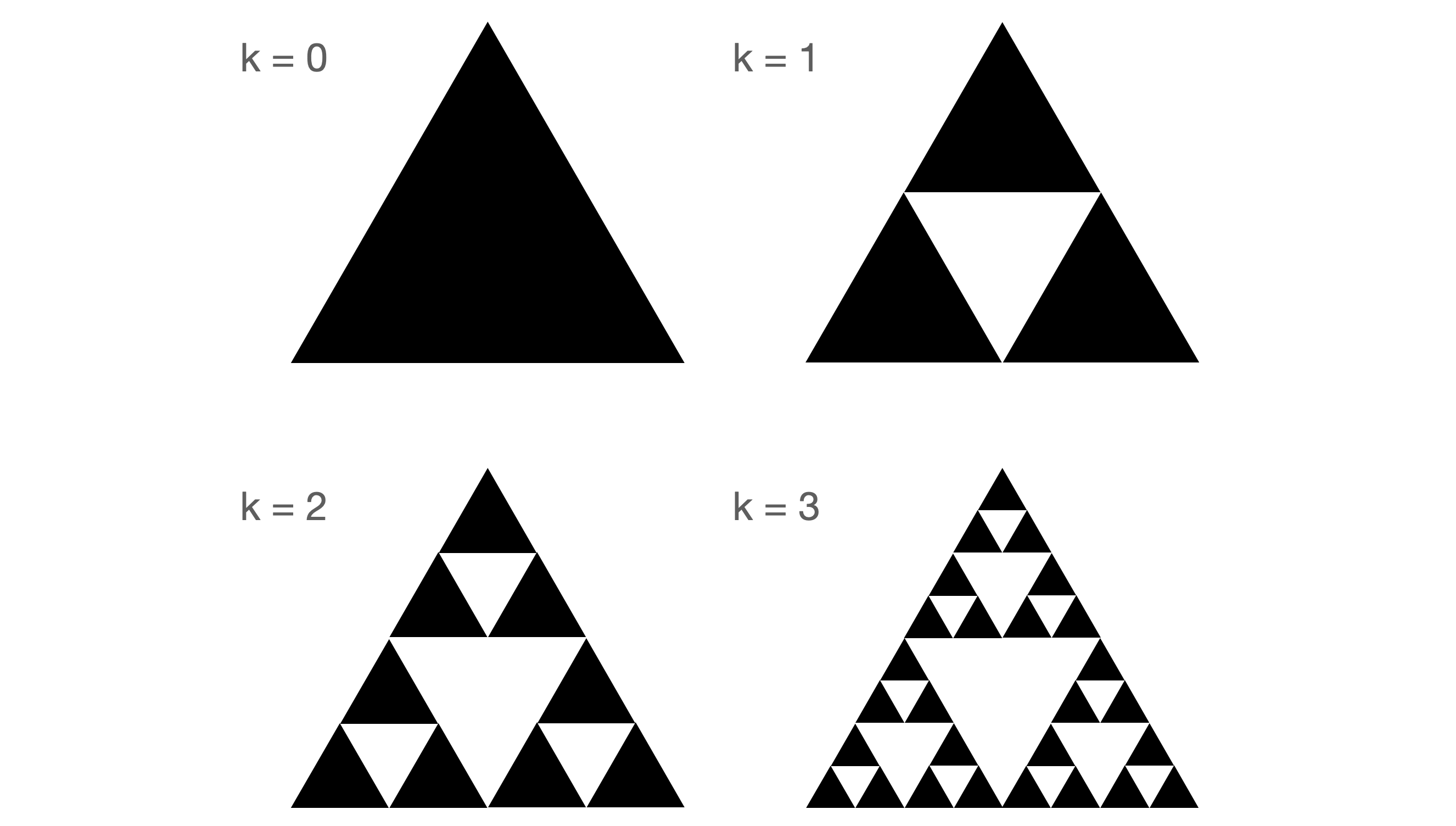
Rysunek 2: Pierwsze cztery iteracje w konstrukcji trójkąta Sierpińskiego