4.3 Pięciokrotka McWortera (ang. McWorter’s pentigree)

William McWorter w 1990 roku zaproponował ciekawą rodzinę fraktali opartą na bardzo prostych geometrycznych transformacjach. Poniższy fraktal wykorzystuje sześć transformacji, z których każda skaluje wyjściową figurę o \(\frac{3 - \sqrt 5}{2} \approx 0,38196\), a następnie obraca o \(36^\circ\); \(108^\circ\); \(-36^\circ\); \(-108^\circ\); \(-36^\circ\) i \(36^\circ\) stopni i odpowiednio ją przesuwa.

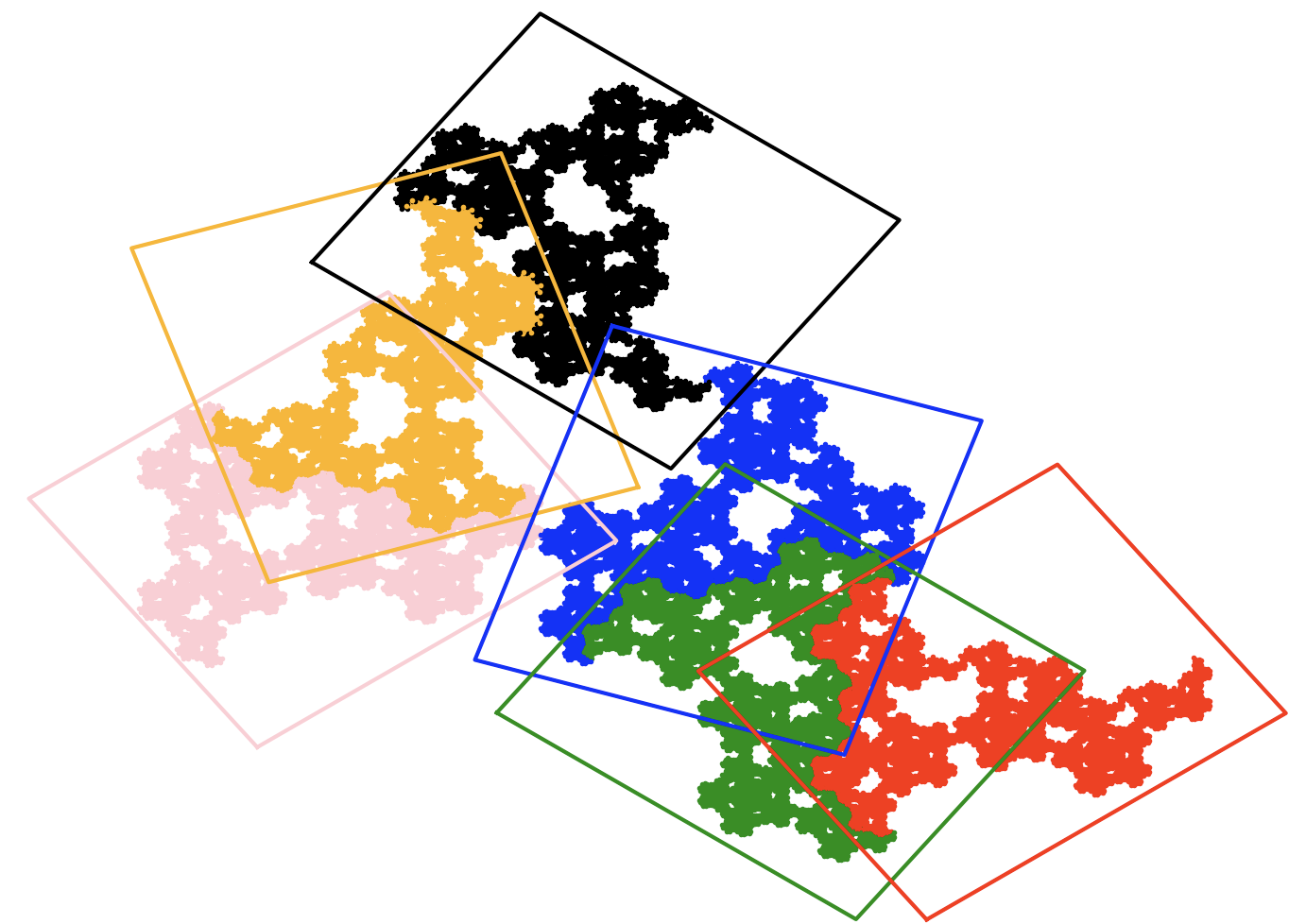
Składowe transformacje dla pięciokrotki McWortera. Kolorem oznaczono obrazy kolejnych transformacji.

Wykres uzyskany algorytmem gry w chaos z prawdopodobieństwami \(1/6\).

\[ f_1(x, y) = \begin{bmatrix} 0,309 & -0,255 & 0 \\ 0,255 & 0,309 & 0 \end{bmatrix} [x \ y \ 1]^T \] \[ f_2(x, y) = \begin{bmatrix} -0,118 & -0,363 & 0,309 \\ 0,363 & -0,118 & 0,225 \end{bmatrix} [x \ y \ 1]^T \] \[ f_3(x, y) = \begin{bmatrix} 0,309 & 0,225 & 0,191 \\ -0,225 & 0,309 & 0,588 \end{bmatrix} [x \ y \ 1]^T \] \[ f_4(x, y) = \begin{bmatrix} -0,118 & 0,363 & 0,500 \\ -0,363 & -0,118 & 0,363 \end{bmatrix} [x \ y \ 1]^T \] \[ f_5(x, y) = \begin{bmatrix} 0,309 & 0,225 & 0,382 \\ -0,225 & 0,309 & 0 \end{bmatrix} [x \ y \ 1]^T \] \[ f_6(x, y) = \begin{bmatrix} 0,309 & -0,225 & 0,691 \\ 0,225 & 0,309 & -0,225 \end{bmatrix} [x \ y \ 1]^T \]