3.2 Gra w Chaos

Sposób generowania fraktali przedstawiony w poprzednim rozdziale opiera się na rekurencji. Składanie transformacji powoduje, że liczba obiektów, które musimy narysować, rośnie wykładniczo. W przypadku paproci, która składa się z czterech transformacji, wygenerowanie paproci na głębokości 10 wymaga narysowania \(4^{10}\) punktów (ponad milion). A 10 poziomów to bardzo mało, jeżeli chcemy uzyskać atrakcyjną grafikę w wysokiej rozdzielczości. Gdybyśmy chcieli wykonać 56 iteracji dla dywanu Sierpińskiego, to musielibyśmy narysować \(8^{56} > 10^{50}\) punktów, czyli więcej niż jest atomów na całej Ziemi!

Okazuje się, że fraktale oparte na składaniu kontrakcji można wygenerować w bardziej kontrolowany sposób. Co więcej, okaże się, że będzie on bazował na generowaniu losowych ruchów.

Czytelniku, to będzie niesamowite! Powtarzanie wielokrotnie losowych ruchów będzie nas prowadziło nieustannie do niezmiennie stałych figur geometrycznych. Okazuje się, że nawet długie losowe trajektorie prowadzić mogą do przewidywalnych wzorców, i to właśnie będzie gra w chaos.

3.2.1 Gra w chaos i trójkąty

Zacznijmy od prostego przykładu, który będzie uogólnioną metodą konstrukcji trójkąta Sierpińskiego. Prześledźmy następujący algorytm.

1. Wybierz trzy dowolne niewspółliniowe punkty na płaszczyźnie. To będą wierzchołki A, B i C trójkąta Sierpińskiego.
2. Wybierz dowolny punkt na płaszczyźnie. To będzie pozycja naszego pióra rysującego fraktal.
3. Wybierz losowo wierzchołek A, B lub C i przesuń pióro o połowę w kierunku wybranego wierzchołka. Powtarzaj to losowanie i przesuwanie w nieskończoność (lub wystarczająco długo).

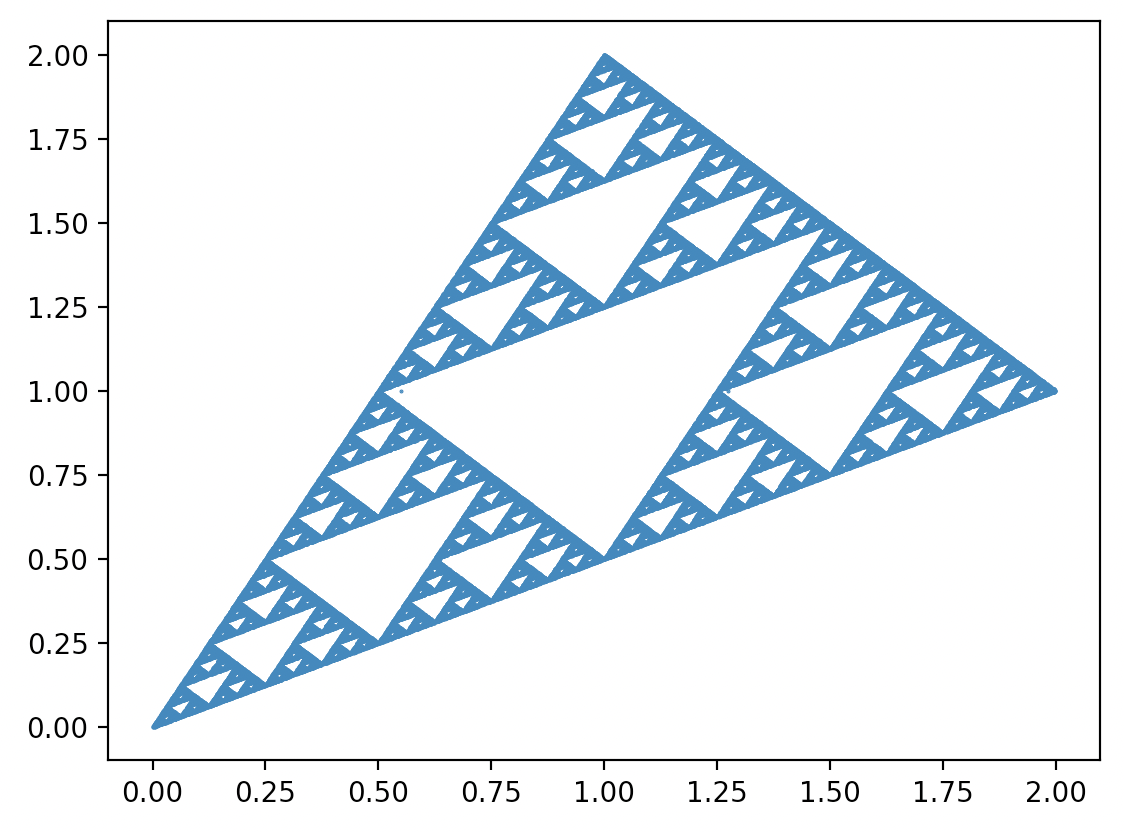
Trojkąt złożony ze 100 000 punktów w grze w chaos

Okazuje się, że gdy będziemy śledzić pozycję pióra, naszym oczom ukaże się trójkąt Sierpińskiego!

3.2.2 Co tu się dzieje?

Zauważ, Drogi Czytelniku, że przesuwanie pióra o połowę odległości w kierunku wybranego wierzchołka jest równoznaczne z wykonaniem transformacji -> pomniejsz obraz o 1/2 i przesuń w kierunku wybranego wierzchołka.

Tak więc w rzeczywistości w losowy sposób wykonujemy jedną z transformacji: (1) pomniejsz 2-krotnie i przesuń w kierunku wierzchołka A, (2) pomniejsz 2-krotnie i przesuń w kierunku wierzchołka B lub (3) pomniejsz 2-krotnie i przesuń w kierunku wierzchołka C.

W poprzednim rozdziale takie transformacje już wykorzystywaliśmy do budowy trójkąta Sierpińskiego. Ale stosowaliśmy jednocześnie wszystkie trzy, składając taką sumę transformacji wielokrotnie.

Okazuje się, że nie musimy wykonywać tych transformacji jednocześnie, wystarczy wylosować jedną i powtarzać to losowanie w nieskończoność.

3.2.3 Gra w Chaos i fraktale

Algorytm generowania z fraktali z użyciem gry w chaos polega na przekształcaniu jednego punktu (pióra) iteracyjnie przez losową wybraną transformację z pewnego zbioru transformacji. Każda transformacja musi być kontrakcją (w przykładach ograniczymy się do przekształceń afinicznych).

Algorytm konstrukcji fraktali oparty na grze w chaos.

1. Wybierz punkt początkowy dla pióra.
2. Ze zbioru transformacji zwężających wylosuj jedną transformację i przekształć współrzędne pióra zgodnie z tą transformacją.
3. Narysuj współrzędną pióra na ekranie.
4. Wróć do kroku 2.

Pokażemy, jak ten algorytm działa na przykładzie konstrukcji paproci Barnsleya, ale dla wygody najpierw przedstawimy alternatywny sposób zapisu transformacji afinicznych.

3.2.4 Przekształcenia afiniczne

W poprzednim rozdziale przekształcenia afiniczne definiowaliśmy przez dowolne złożenie trzech rodzajów transformacji – przesunięcia, obrotu oraz skalowania (w tym odbicia pionowego lub poziomego), przy czym skalowanie musiało mieć skalę mniejszą niż 1 co do wartości bezwzględnej, aby było zwężające. Taka reprezentacja jest wygodna dla ludzi, ponieważ łatwo na jej podstawie wyobrazić sobie, co się dzieje z wyjściowymi figurami. Okazuje się jednak, że dla komputera znacznie wygodniejszą reprezentacją przekształcenia afinicznego jest postać macierzowa transformacji.

W zapisie macierzowym każdą transformację afiniczną \((x', y') = f(x, y)\) w przestrzeni dwuwymiarowej można przedstawić za pomocą sześciu liczb \((a, b, c, d, e, f)\).

\[ \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ d & e \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} c \\ f \end{bmatrix} = \begin{bmatrix} a x + b y + c \\ d x + e y + f \end{bmatrix}. \]

Jeżeli znamy podstawy algebry macierzowej, to z reprezentacji opartej na obrotach, przesunięciach i skalowaniu możemy łatwo wyliczyć współczynniki \(a\)–\(f\). Kilka przykładów odpowiadających sobie reprezentacji przekształceń afinicznych znajduje się w kolejnym rozdziale.

Teraz jednak zobaczmy, jak przy użyciu gry w chaos skonstruować paproć.

3.2.5 Paprocie i chaos

Tabela 1 przedstawia cztery transformacje afiniczne zapisane za pomocą notacji macierzowej.

	a	b	c	d	e	f
\(T_1\): łodyżka	0,00	0,00	0	0,00	0,16	0,00
\(T_2\): góra	0,85	0,04	0	$-$0,04	0,85	1,60
\(T_3\): lewy liść	0,20	$-$0,26	0	0,23	0,22	0,80
\(T_4\): prawy liść	$-$0,15	0,28	0	0,26	0,24	0,44

[Współczynniki transformacji składających się na paproć Barnsleya]

Aby narysować paproć z poniższego rysunku, wystarczy wziąć losowy punkt, a następnie 100 000 razy powtórzyć trzy kroki: wylosować jedną z transformacji z tej tabeli, stosując prawdopodobieństwa losowania 1%, 79%, 10%, 10% dla kolejnych transformacji, przekształcić współrzędne punktu wylosowaną transformacją, narysować punkt na wykresie.

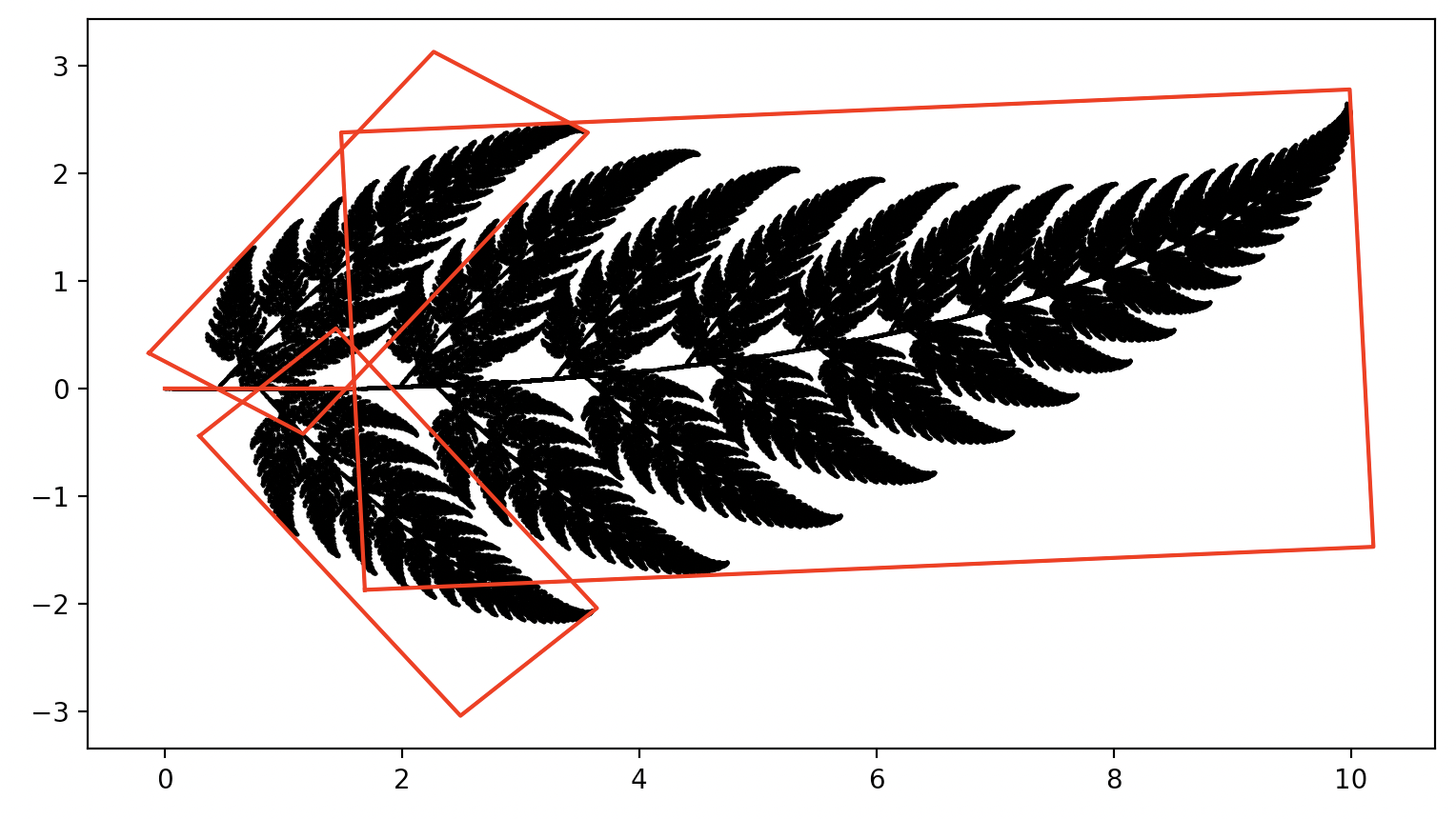
Ilustracja czterech transformacji (obrysowanych czerwonymi prostokątami) na bazie paproci Barnsleya

Przy okazji widać, że mamy olbrzymią redukcję informacji – taką piękną paproć opisaliśmy wyłącznie z użyciem 24 liczb. Ta obserwacja stała się fundamentem kompresji fraktalnej, dziedziny, która zamierzała zmniejszyć istotnie opis graficznych figur, stosując ich reprezentację fraktalną.

Częściej losujemy lewy i prawy liść, rzadziej górę

Częściej losujemy łodyżkę, znacznie rzadziej liście

Nie losujemy łodyżki

Wybór punktu \(x_0\) nie ma znaczenia, ale jeżeli bardzo odstaje od fraktala, to z przyczyn wizualnych warto pominąć kilka pierwszych kroków gry w chaos, tak by żadne punkty za bardzo nie odstawały od głównego obrazu.

Jaką rolę odgrywają prawdopodobieństwa w tworzeniu fraktala?

Zauważmy, że prawdopodobieństwo wylosowania łodyżki jest mniejsze niż głównej części paproci, również dlatego, że łodyżka zajmuje mało miejsca i nie ma co marnować czasu, losując punkty z łodyżki.

Na marginesie możemy przyjrzeć się trzem różnym paprociom Barnsleya, które składają się z tych samych transformacji, przedstawionych w tabeli 1, ale w których zastosowano różne prawdopodobieństwa. Ogólny zarys każdej z tych paproci jest podobny, ale widzimy, że sterując prawdopodobieństwami, możemy otrzymać mniej lub bardziej ażurowe konstrukcje.

3.2.6 Bardziej formalnie

Jeżeli już mamy zbudowaną intuicję, jak działa gra w chaos, to warto zapisać to, co się wydarzyło, bardziej formalnie.

Mamy zbiór \(K\) przekształceń \(f_i:R^2 \rightarrow R^2\), które są przekształceniami zwężającymi, czyli spełniającymi warunek:

\[ \exists_{\lambda < 1}\forall_{x, y} \lambda d(x,y) \geq d(f(x), f(y)). \]

Mamy wektor \(K\) prawdopodobieństw wylosowania kolejnych przekształceń \(\pi_i \geq 0\). Prawdopodobieństwa sumują się do 1, czyli \(\sum_{i=1}^K \pi_i = 1\).

Ciąg punktów \(x_0\), \(f_{a_1}(x_0)\), \(f^2(x_0) = f_{a_2}(f_{a_1}(x_0))\), \(f^3(x_0) = f_{a_3}(f_{a_2}(f_{a_1}(x_0)))\), … tworzy obraz fraktala. Symbol \(a_i\) oznacza i-tą wylosowaną wartość ze zbioru \(1...K\) przy losowaniu z prawdopodobieństwem \(\pi_1, ..., \pi_K\).

Wybór punktu \(x_0\) nie ma znaczenia.