2.5 Przykłady w języku R
Przykłady przedstawione w tym rozdziale powtarzają złożenie trzech atomowych transformacji – przesunięcia, przeskalowania i obrotu.
Poniżej znajdują się definicje tych trzech transformacji. W tych przykładach x jest dwuelementowym wektorem.
# Przesunięcie punktu x o delta.
shift = function(x, delta)
x + delta
# Przeskalowanie punktu x razy ratio.
scale = function(x, ratio)
x * ratio
# Obrót o kąt alpha (w stopniach).
rotate = function(x, alpha) {
sa = sin(pi * alpha / 180)
ca = cos(pi * alpha / 180)
x %*% matrix(c(ca, -sa, sa, ca), 2, 2, byrow = TRUE)
}2.5.1 Trójkąt Sierpińskiego
Trójkąt Sierpińskiego składa się z trzech transformacji.
\[ y_1 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] \]
\[ y_2 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] + \left[\begin{smallmatrix} 0.5 \\ 0 \end{smallmatrix}\right] \]
\[ y_3 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] + \left[\begin{smallmatrix} 0.25 \\ \sqrt3/4 \end{smallmatrix}\right] \]
Tak jak napisaliśmy na początku tego rozdziału, fraktale możemy budować ze zwykłych kropek, nie potrzebujemy bardziej wyrafinowanych poligonów. Przedstawmy to na bazie trójkąta Sierpińskiego.
# Zapis x |> scale(0.5) |> shift(0.2) w języku R oznacza
# ogonowe złożenie tych funkcji i jest równoważny zapisowi
# shift(scale(x, 0.5), 0.2). Jest jednak czytelniejszy.
sierpinski <- function(x, depth, col = "black") {
if (depth > 1) {
x1 = x |> scale(0.5)
sierpinski(x1, depth - 1, col = "blue")
x2 = x |> scale(0.5) |> shift(c(0.5, 0))
sierpinski(x2, depth - 1, col = "red")
x3 = x |> scale(0.5) |> shift(c(0.25, 0.5))
sierpinski(x3, depth - 1, col = "orange")
} else {
points(x[1], x[2], pch = 19, col = col, cex=0.3)
}
}
plot.new()
plot.window(xlim=c(0, 1), ylim=c(0,1), asp=1)
sierpinski(c(0,0), depth = 8)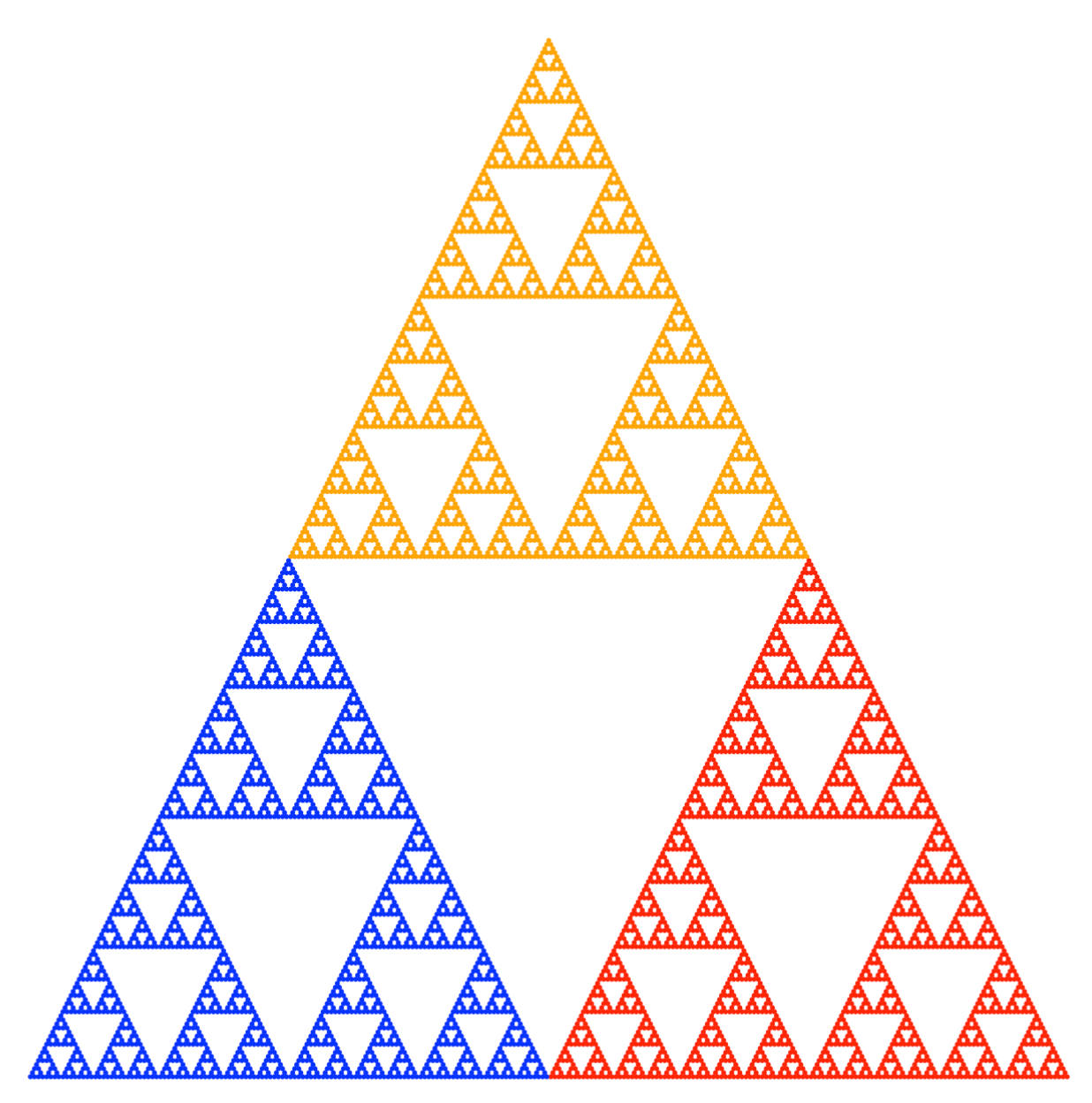
Wynik wykonania powyższych instrukcji
2.5.2 Pięciokąt Sierpińskiego
pentagon <- function(x, depth, color="black") {
if (depth > 1) {
x1 = x |> scale(0.382)
pentagon(x1, depth - 1, color = "blue")
x2 = x |> scale(0.382) |> shift(c(0.618, 0))
pentagon(x2, depth - 1, color = "red")
x3 = x |> scale(0.382) |> shift(c(0.809, 0.588))
pentagon(x3, depth - 1, color = "green")
x4 = x |> scale(0.382) |> shift(c(0.309, 0.951))
pentagon(x4, depth - 1, color = "orange")
x5 = x |> scale(0.382) |> shift(c(-0.191, 0.588))
pentagon(x5, depth - 1, color = "pink")
} else
points(x[1], x[2], pch = 19, col = color, cex=0.5)
}
plot.new()
plot.window(xlim=c(-0.5,1.5), ylim=c(-0.1,1.7), asp=1)
pentagon(c(0,0), depth = 6)
Wynik wykonania powyższych instrukcji
2.5.3 Smok Heighwaya
heighway <- function(x, depth, color="black") {
if (depth > 1) {
x1 = x|> rotate(45)|> scale(sqrt(0.5))|> shift(c(1,0))
heighway(x1, depth-1, color="blue")
x2 = x|> rotate(45)|> scale(sqrt(0.5))
heighway(x2, depth-1, color="red")
} else
points(x[1], x[2], pch=19, col=color, cex=0.5)
}
plot.new()
plot.window(xlim=c(-1,2), ylim=c(-1.5,0.5), asp=1)
heighway(c(1,1), depth = 15)
Wynik wykonania powyższych instrukcji
2.5.4 Symetryczne drzewo binarne / drzewo Pitagorasa
pitagoras = function(x, depth, color="black") {
if (depth > 1) {
x1 = x|> rotate(-45) |> scale(sqrt(0.5)) |> shift(c(0,1))
pitagoras(x1, depth-1, color="blue")
x2 = x|> rotate(45) |> scale(sqrt(0.5)) |> shift(c(0,1))
pitagoras(x2, depth-1, color="red")
} else
points(x[1], x[2], pch=19, col=color, cex=0.5)
}
plot.new()
plot.window(xlim = c(-3,3), ylim = c(0,3), asp=1)
pitagoras(c(1,1), depth = 15)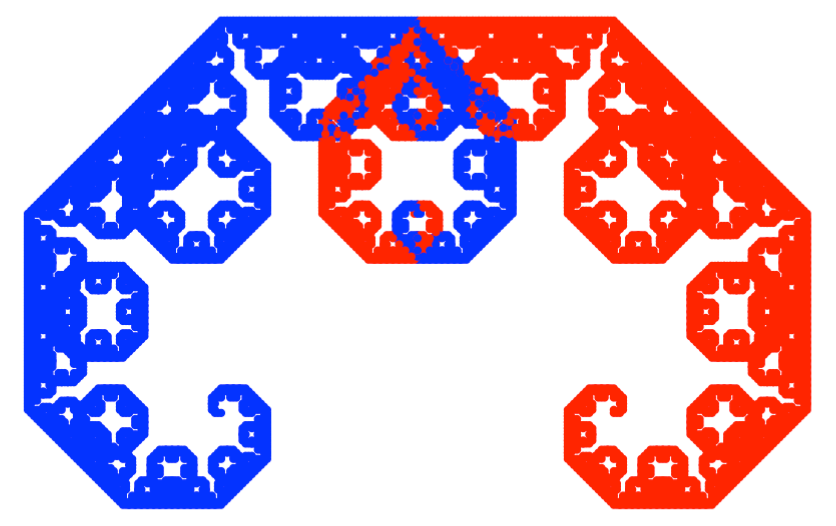
Wynik wykonania powyższych instrukcji