2.4 Przykłady w języku Python

Przykłady przedstawione w tym rozdziale powtarzają złożenie trzech atomowych transformacji – przesunięcia, przeskalowania i obrotu.

Poniżej znajdują się definicje tych trzech przekształceń. W poniższych przykładach x jest dwuelementowym wektorem.

import numpy as np
import matplotlib.pyplot as plt

# Przesunięcie punktu x o wektor delta.
def shift(x, delta): 
    return np.add(x, delta)

# Przeskalowanie punktu x razy ratio.
def scale(x, ratio): 
    return np.multiply(x, ratio)

# Obrót o kąt alpha (w stopniach).
def rotate(x, alpha): 
    adeg = math.pi * alpha / 180
    rotation_matrix = [
          [np.cos(adeg), -np.sin(adeg)],
          [np.sin(adeg), np.cos(adeg)]]
    return np.matmul(x, rotation_matrix)

2.4.1 Trójkąt Sierpińskiego

Tak jak napisaliśmy na początku tego rozdziału, fraktale możemy budować ze zwykłych kropek, nie potrzebujemy bardziej wyrafinowanych poligonów. Przedstawmy to na bazie trójkąta Sierpińskiego.

Trójkąt Sierpińskiego składa się z trzech transformacji.

\[ y_1 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] \]

\[ y_2 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] + \left[\begin{smallmatrix} 0.5 \\ 0 \end{smallmatrix}\right] \]

\[ y_3 = x * \left[\begin{smallmatrix} 0.5 & 0\\ 0 & 0.5 \end{smallmatrix}\right] + \left[\begin{smallmatrix} 0.25 \\ \sqrt3/4 \end{smallmatrix}\right] \]

import matplotlib.pyplot as plt
import numpy as np

# przesunięcie punktu x o delta
def shift(x, delta):
    return np.add(x, delta)

# przeskalowanie punktu x razy ratio
def scale(x, ratio):
    return np.multiply(x, ratio)

# Poniższy program powtarza złożenie tych funkcji depth razy.
# W teorii robilibyśmy to w nieskończoność, ale do uzyskania
# wyraźnego obrazka wystarczy kilka kroków. 
# Liczba punktów rośnie wykładniczo, więc po k krokach wynosi 3^k.
def sierpinski(x, depth): 
    if depth > 1: 
        x1 = scale(shift(x,  [0, 0]), [0.5, 0.5])
        sierpinski(x1, depth - 1)
        x2 = scale(shift(x,  [0.5, 0]), [0.5, 0.5])
        sierpinski(x2, depth - 1)
        x3 = scale(shift(x,  [0.25, 0.5]), [0.5, 0.5])
        sierpinski(x3, depth - 1)
    else:
        plt.plot(x[0], x[1], marker='o', 
                color="black", markersize=3)

# Inicjacja rysunku i narysowanie trójkąta Sierpińskiego.
plt.figure()   
sierpinski([0,0], depth = 7)
plt.show()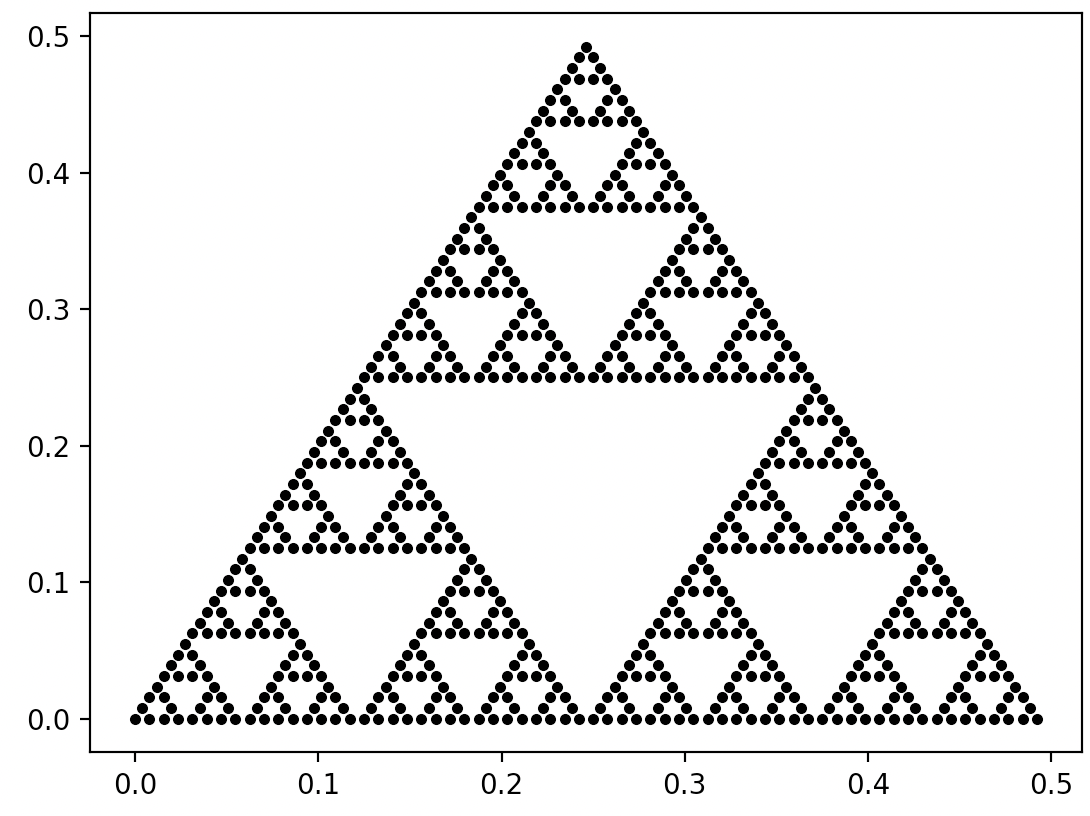

Wynik wykonania powyższych instrukcji

2.4.2 Pięciokąt Sierpińskiego

import math
import numpy as np
import matplotlib.pyplot as plt

# przesunięcie punktu x o delta
def shift(x, delta):
    return np.add(x, delta)

# przeskalowanie punktu x razy ratio
def scale(x, ratio):
    return np.multiply(x, ratio)

def pentagon(x, depth, col="black"):
    if depth > 1: 
        x1 = shift(scale(x, [0.382,0.382]), [0,0])
        pentagon(x1, depth-1, col="red")
        x2 = shift(scale(x, [0.382,0.382]), [0.618,0])
        pentagon(x2, depth-1, col="blue")
        x3 = shift(scale(x, [0.382,0.382]), [0.809,0.588])
        pentagon(x3, depth-1, col="green")
        x4 = shift(scale(x, [0.382,0.382]), [0.309,0.951])
        pentagon(x4, depth-1, col="orange")
        x5 = shift(scale(x, [0.382,0.382]), [-0.191,0.588])
        pentagon(x5, depth-1, col="brown")
    else:
        plt.plot(x[0],x[1], marker='o', color=col, markersize=3)

plt.figure()
pentagon([0,0], depth=6, col)
plt.show()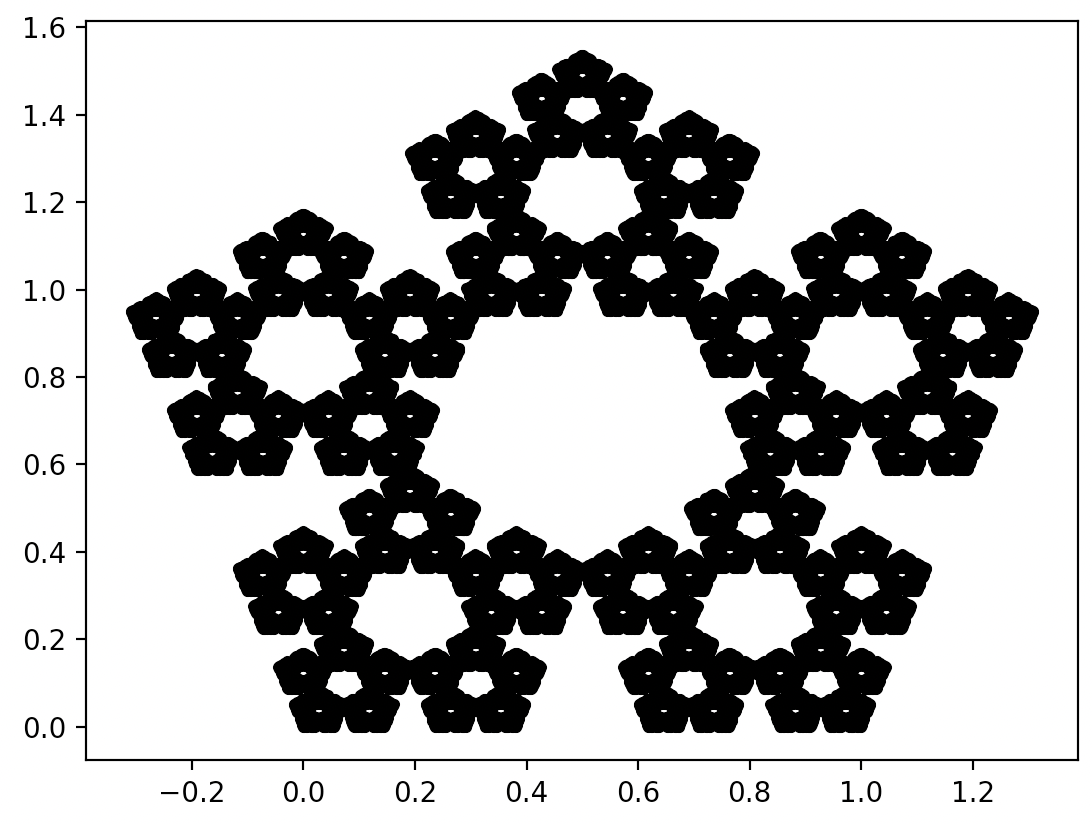

Wynik wykonania powyższych instrukcji

2.4.3 Smok Heighwaya

import math
import numpy as np
import matplotlib.pyplot as plt

import numpy as np
import matplotlib.pyplot as plt

# Przesunięcie punktu x o wektor delta.
def shift(x, delta): 
    return np.add(x, delta)

# Przeskalowanie punktu x razy ratio.
def scale(x, ratio): 
    return np.multiply(x, ratio)

# Obrót o kąt alpha (w stopniach).
def rotate(x, alpha): 
    adeg = math.pi * alpha / 180
    rotation_matrix = [
          [np.cos(adeg), -np.sin(adeg)],
          [np.sin(adeg), np.cos(adeg)]]
    return np.matmul(x, rotation_matrix)
  
def heighway(x, depth, col="black"):
    if depth > 1: 
        x1 = rotate(x, -45)
        x1 = scale(x1, [np.sqrt(0.5), np.sqrt(0.5)])
        heighway(x1, depth-1, col="blue")
        x2 = rotate(x, -45)
        x2 = scale(x2, [np.sqrt(0.5), np.sqrt(0.5)])
        x2 = shift(x2, [0.75, 0.25])
        heighway(x2, depth-1, col="red")
    else:
        plt.plot(x[0], x[1], marker='o', color=col, markersize=3)

plt.figure()
heighway([0,0], depth=14)
plt.show()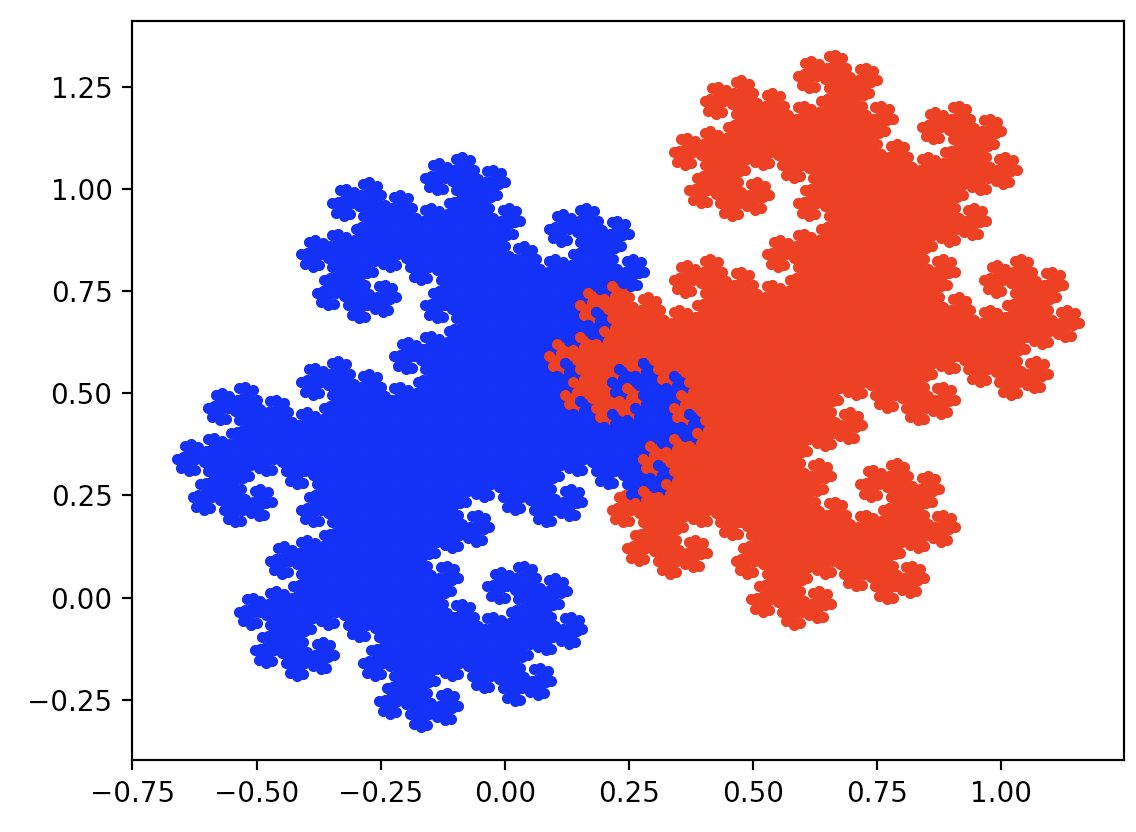

Wynik wykonania powyższych instrukcji

2.4.4 Drzewo Pitagorasa

import numpy as np
import matplotlib.pyplot as plt

# Przesunięcie punktu x o wektor delta.
def shift(x, delta): 
    return np.add(x, delta)

# Przeskalowanie punktu x razy ratio.
def scale(x, ratio): 
    return np.multiply(x, ratio)

# Obrót o kąt alpha (w stopniach).
def rotate(x, alpha): 
    adeg = math.pi * alpha / 180
    rotation_matrix = [
          [np.cos(adeg), -np.sin(adeg)],
          [np.sin(adeg), np.cos(adeg)]]
    return np.matmul(x, rotation_matrix)
  
def sbt(x, depth, col="black"):
    if depth > 1: 
        x1 = rotate(x, -45)
        x1 = shift(scale(x1, [0.7, 0.7]), [0, 1])
        sbt(x1, depth-1, col="blue")
        x2 = rotate(x, 45)
        x2 = shift(scale(x2, [0.7, 0.7]), [0, 1])
        sbt(x2, depth-1, col="red")
    else:
        plt.plot(x[0], x[1], marker='o', color=col, markersize=3)

plt.figure()
sbt([0,0], depth = 14)
plt.show()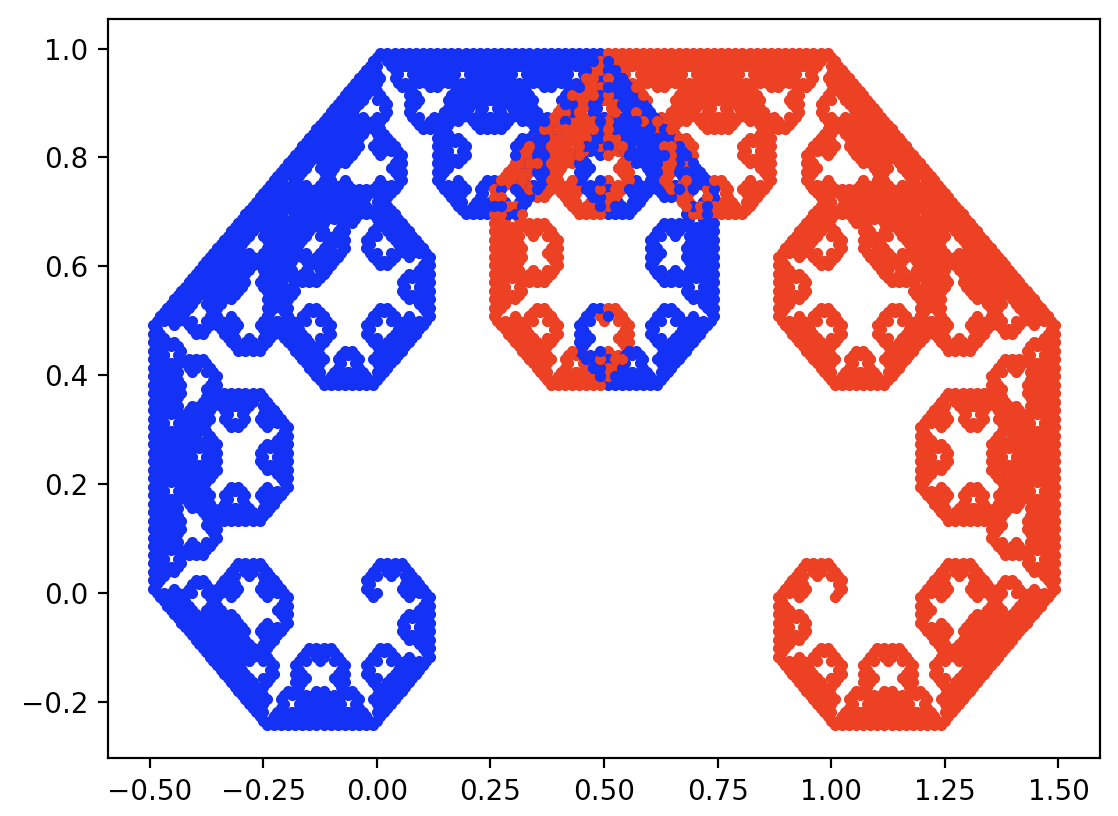

Wynik wykonania powyższych instrukcji