3.6 Przykłady w języku Julia
3.6.1 Trójkąt Sierpińskiego raz jeszcze
Poniższy kod odtwarza konstrukcję trójkąta Sierpińskiego przedstawioną w tym rozdziale. W macierzy triangle definiujemy trzy wierzchołki trójkąta, a w obiekcie point umieszczamy współrzędne punktu startowego dla konstrukcji fraktala. Następnie w pętli przesuwamy punkt w kierunku losowego wierzchołka.
- \(x' = x/2\), \(y' = y/2\) (lewy róg)
- \(x' = x/2 + \frac 12\), \(y' = y/2\) (prawy róg)
- \(x' = x/2 + \frac 14\), \(y' = y/2 + \frac{\sqrt{3}}2\) (górny róg)
using Plots
# Liczba kroków, wierzchołki trójkąta i kolory dla transformacji.
N = 100000
triangle = [0 0; 0.5 2; 1.5 0.5]
col = ["red" "green" "blue"]
point = [0.1 0]
# Macierz na kolejne punkty trójkąta Sierpińskiego.
points = zeros(N, 2)
cols = String[]
# Wektor cols zbiera kolory odpowiadające wylosowanym
# transformacjom a macierz coords zbiera współrzędne
# pióra po każdym skoku.
for i in 1:N
ind = rand(1:3,1)
append!(cols, col[ind])
point = (point + triangle[ind, :])/2
coords[i,:] = point
end
scatter(coords[:,1], coords[:,2], color=cols,
legend=:false, markersize=2, axis=nothing)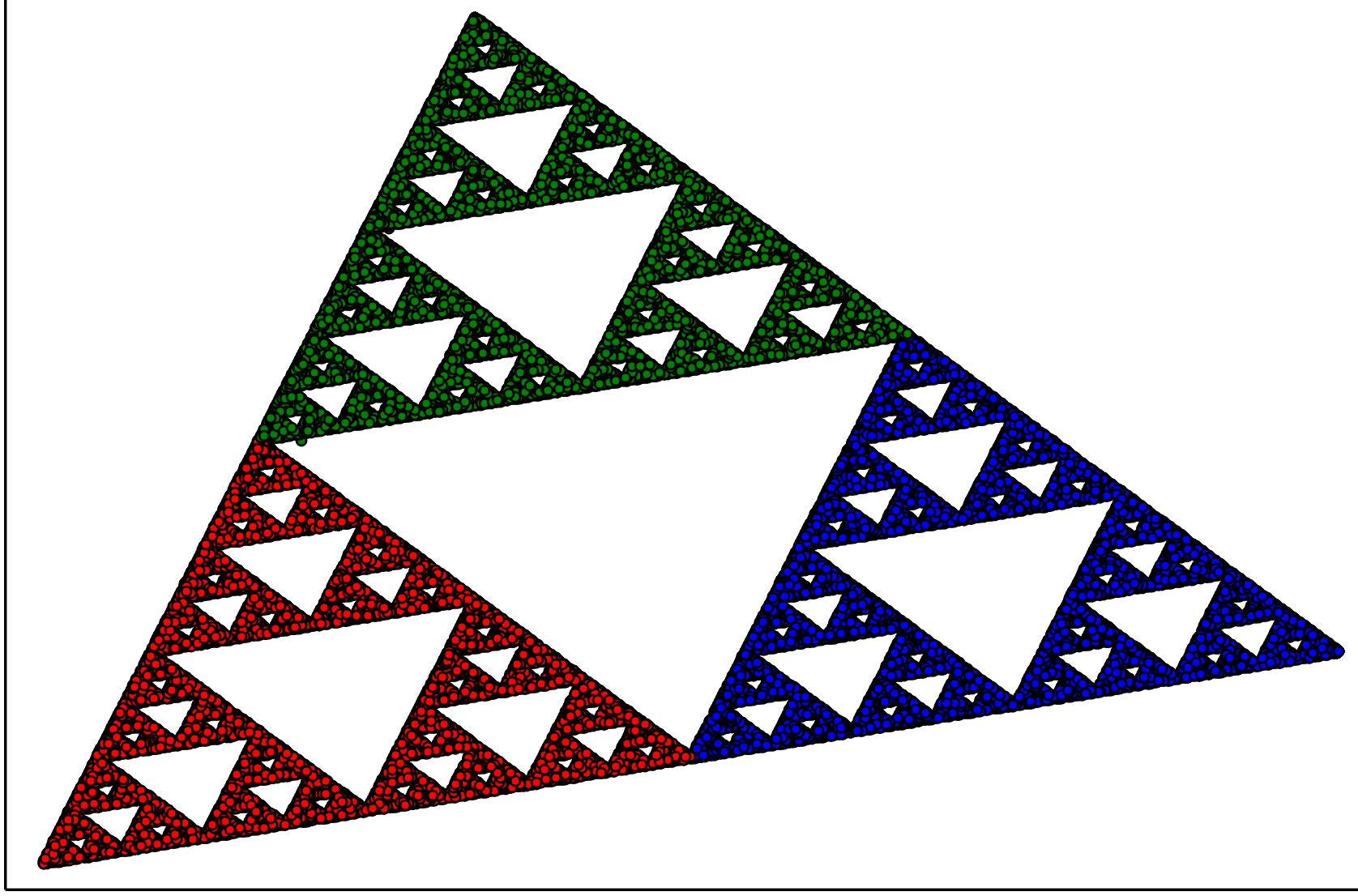
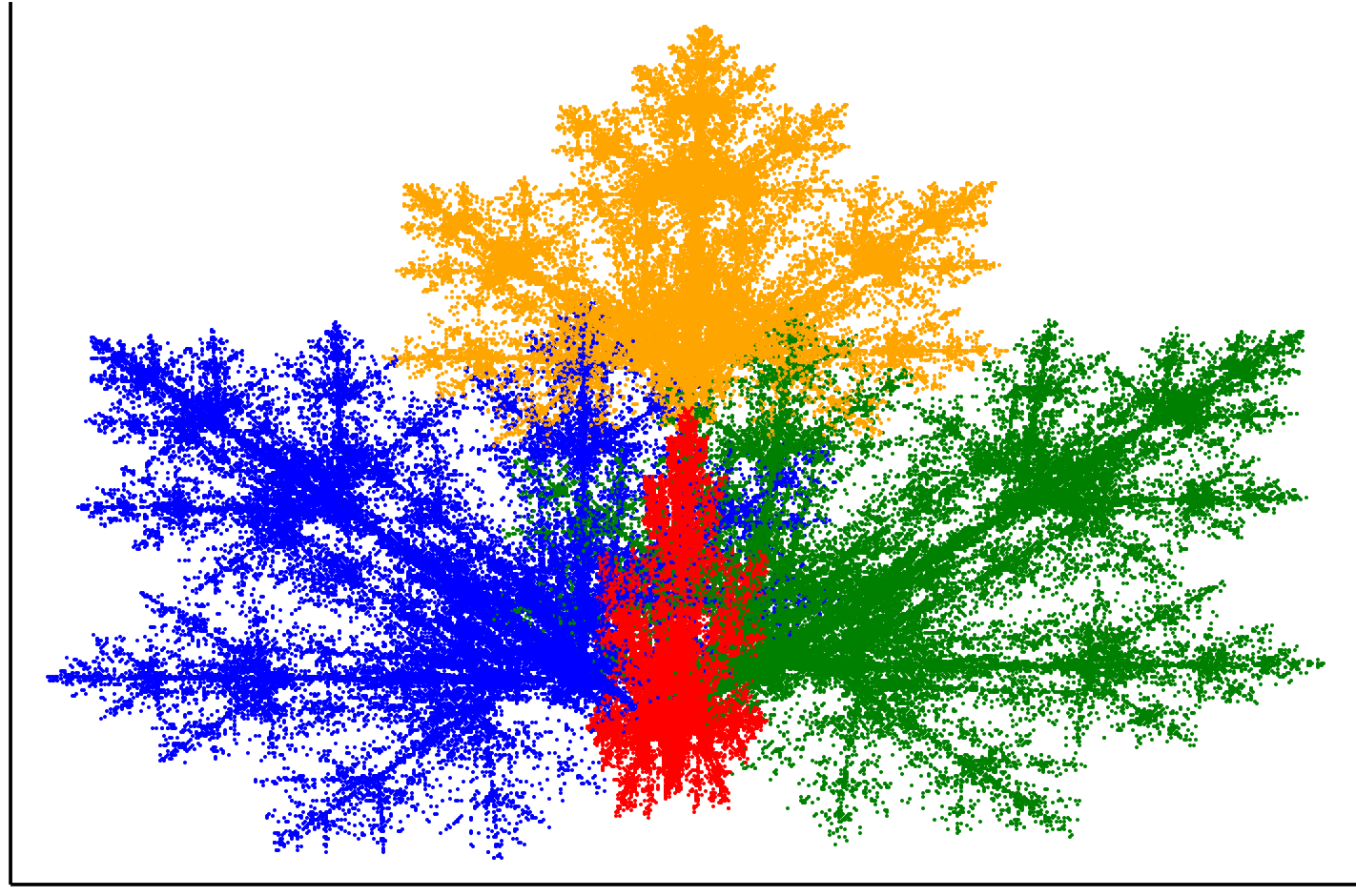
3.6.2 Paproć Barnsleya
using StatsBase
# Kolejne transformacje są zapisane jako osobne funkcje,
# które później złożą się na wektor funkcji trans.
trans1(x) = [ 0. 0.; 0. 0.16]*x
trans2(x) = [0.85 0.04; -0.04 0.85]*x + [0; 1.6]
trans3(x) = [0.2 -0.26; 0.23 0.22]*x + [0; 0.8]
trans4(x) = [-0.15 0.28; 0.26 0.24]*x + [0; 0.44]
trans = [trans1, trans2, trans3, trans4]
point = [0 0]'
col = ["red" "green" "blue" "orange"]
probs = [0.01, 0.79, 0.1, 0.1]
N = 200000
coords = zeros(N, 2)
cols = String[]
for i in 1:N
# Losujemy transformacje wykorzystując wektor *probs* z częstościami
# występowania poszczególnych transformacji. Funkcja sample
# jest dostępna w bibliotece StatsBase.
ind = sample(1:length(probs), Weights(probs))
selected_trans = trans[ind[1]]
point = selected_trans(point)
coords[i,:] = point
push!(cols, col[ind])
end
scatter(coords[:,1], coords[:,2], color=cols,
legend=:false, markersize=1, axis=nothing,
markerstrokecolor=cols)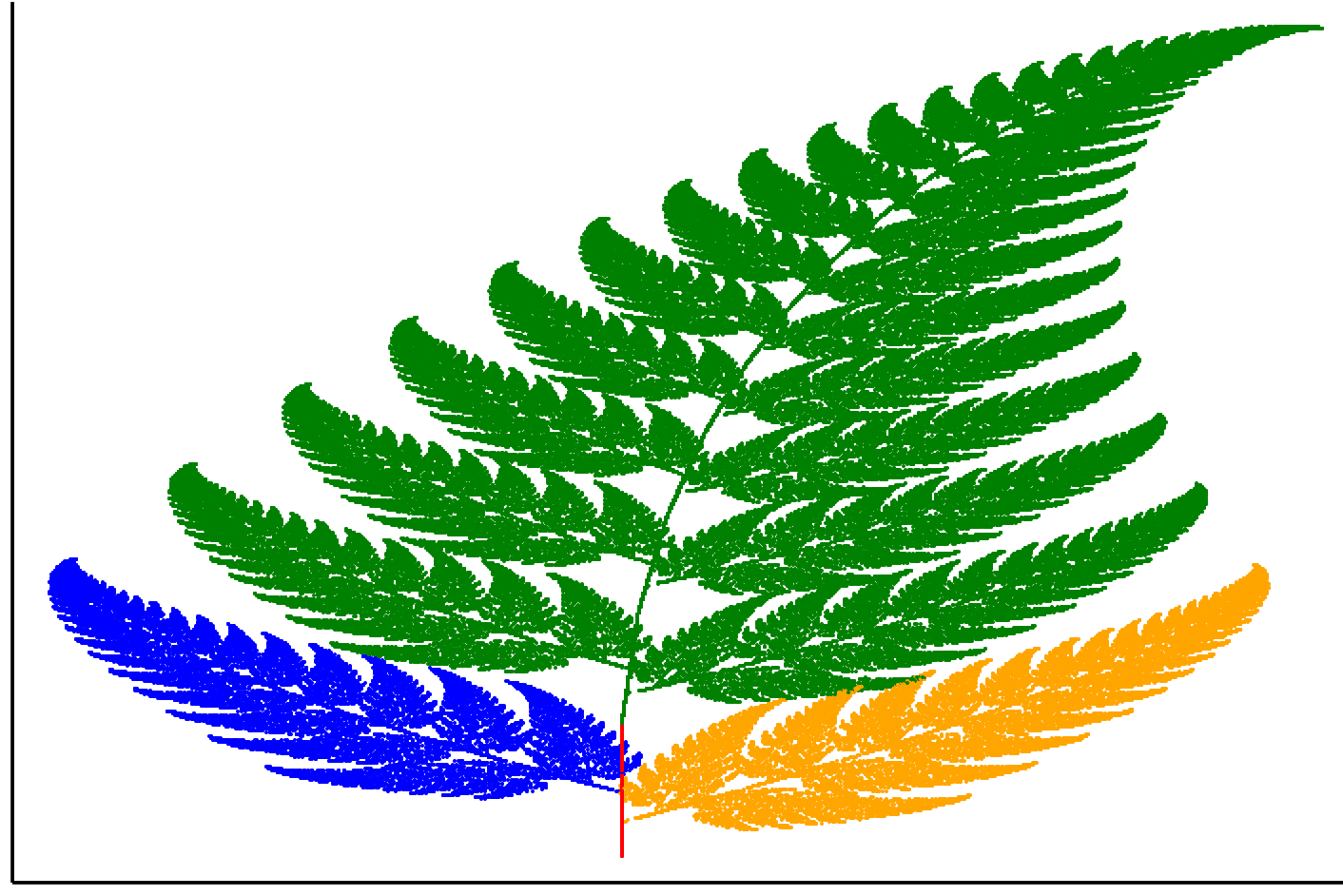
3.6.3 Liść klonu
# Kolejne transformacje zapisujemy jako macierze 3x3 przekształceń
# liniowych. Przez co zapis jest bardziej kompaktowy.
affines = [[0.14 0.01 -0.08; 0.0 0.51 -1.31; 0 0 1],
[0.43 0.52 1.49; -0.45 0.5 -0.75 ; 0 0 1],
[0.45 -0.49 -1.62; 0.47 0.47 -0.74; 0 0 1],
[0.49 0.0 0.02; 0.0 0.51 1.62 ; 0 0 1]]
probs = [0.25, 0.25, 0.25, 0.25]
col = ["red", "green", "blue", "orange"]
N = 200000
point = [0 0 1]'
coords = zeros(N, 2)
cols = String[]
for i in 1:N
# W przeciwieństwie do poprzednich rozdziałów, tutaj nie
# korzystamy z rekurencji. Iteracyjnie liczymy pozycje dla
# N skoków a później wszystkie wyznaczone punkty rysujemy
# jedną instrukcją scatter.
ind = sample(1:length(probs), Weights(probs))
point = affines[ind[1]] * point
coords[i,:] = point[1:2]
push!(cols, col[ind])
end
scatter(coords[:,1], coords[:,2], color=cols,
legend=:false, markersize=1, axis=nothing,
markerstrokecolor=cols)